CH10-图遍历

深度优先搜索

假设初始状态是图中所有顶点均未被访问，则从某个顶点 V 出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索来遍历整个图，直至图中所有和 V 有路径相通的顶点都被访问到。这里的关键是访问到邻接点时，接着去访问该邻接点的所有邻接点，然后再去访问第一层邻接点中的下一个邻接点的所有邻接点。

若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程。

深度优先搜索：无向图

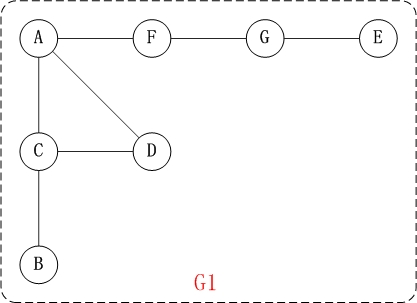
对上面的图G1进行深度优先遍历，从顶点A开始。

1. 访问 A。
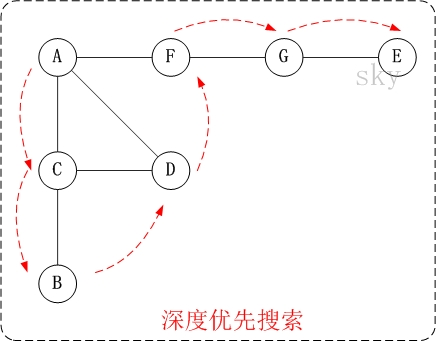
2. 访问(A的邻接点)C。 在第1步访问A之后，接下来应该访问的是A的邻接点，即"C,D,F"中的一个。但在本文的实现中，顶点ABCDEFG是按照顺序存储，C在"D和F"的前面，因此，先访问C。
3. 访问(C的邻接点)B。 在第2步访问C之后，接下来应该访问C的邻接点，即"B和D"中一个(A已经被访问过，就不算在内)。而由于B在D之前，先访问B。
4. 访问(C的邻接点)D。 在第3步访问了C的邻接点B之后，B没有未被访问的邻接点；因此，返回到访问C的另一个邻接点D。
5. 访问(A的邻接点)F。 前面已经访问了A，并且访问完了"A的邻接点B的所有邻接点(包括递归的邻接点在内)"；因此，此时返回到访问A的另一个邻接点F。
6. 访问(F的邻接点)G。
7. 访问(G的邻接点)E。

因此访问顺序是: A -> C -> B -> D -> F -> G -> E

深度优先搜索：有向图

下面以"有向图"为例，来对深度优先搜索进行演示。

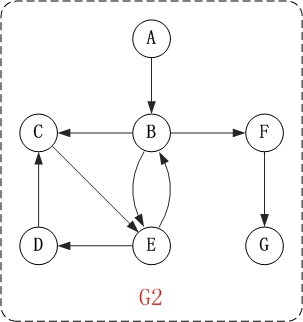
对上面的图G2进行深度优先遍历，从顶点A开始。

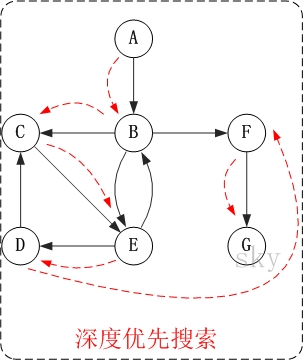
1. 访问A。
2. 访问B。 在访问了A之后，接下来应该访问的是A的出边的另一个顶点，即顶点B。
3. 访问C。 在访问了B之后，接下来应该访问的是B的出边的另一个顶点，即顶点C,E,F。在本文实现的图中，顶点ABCDEFG按照顺序存储，因此先访问C。
4. 访问E。 接下来访问C的出边的另一个顶点，即顶点E。
5. 访问D。 接下来访问E的出边的另一个顶点，即顶点B,D。顶点B已经被访问过，因此访问顶点D。
6. 访问F。 接下应该回溯"访问A的出边的另一个顶点F"。
7. 访问G。

因此访问顺序是: A -> B -> C -> E -> D -> F -> G

广度优先搜索

广度优先搜索算法(Breadth First Search)，又称为"宽度优先搜索"或"横向优先搜索"，简称BFS。

它的思想是: 从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。

广度优先搜索：无向图

下面以"无向图"为例，来对广度优先搜索进行演示。还是以上面的图G1为例进行说明。

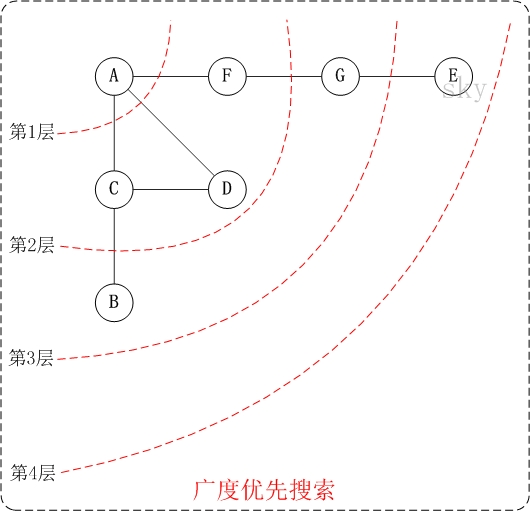
1. 访问 A。
2. 依次访问C,D,F。 在访问了A之后，接下来访问A的邻接点。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，C在"D和F"的前面，因此，先访问C。再访问完C之后，再依次访问D,F。
3. 依次访问B,G。 在第2步访问完C,D,F之后，再依次访问它们的邻接点。首先访问C的邻接点B，再访问F的邻接点G。
4. 访问E。 在第3步访问完B,G之后，再依次访问它们的邻接点。只有G有邻接点E，因此访问G的邻接点E。

因此访问顺序是: A -> C -> D -> F -> B -> G -> E

广度优先搜索：有向图

下面以"有向图"为例，来对广度优先搜索进行演示。还是以上面的图G2为例进行说明。

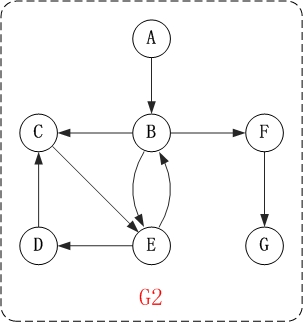
1. 访问A。
2. 访问B。
3. 依次访问C,E,F。 在访问了B之后，接下来访问B的出边的另一个顶点，即C,E,F。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，因此会先访问C，再依次访问E,F。
4. 依次访问D,G。 在访问完C,E,F之后，再依次访问它们的出边的另一个顶点。还是按照C,E,F的顺序访问，C的已经全部访问过了，那么就只剩下E,F；先访问E的邻接点D，再访问F的邻接点G。

因此访问顺序是: A -> B -> C -> E -> F -> D -> G