CH06-红黑树

红黑树和AVL树的思想是类似的，都是在插入过程中对二叉排序树进行调整，从而提升性能，它的增删改查均可以在 O(lg n) 内完成。

定义

红黑树是一棵二叉排序树。且满足以下特点：

• 每个节点或者是黑色，或者是红色。
• 根节点是黑色。
• 每个叶子节点（NIL）是黑色。(注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！)
• 如果一个节点是红色的，则它的两个儿子都是黑色的。
• 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

示例中每个结点最后都是一个 NIL 结点，它是黑色的，不过我们画图时通常会省略它。所以下文以及后续文章中绘制时都会省略NIL结点，大家记得还有它就可以。

实现原理

红黑树的插入与删除和AVL树类似，也是每插入一个结点，都检查是否破坏了树的结构，然后进行调整。红黑树每个结点插入时默认都为红色，这样做可以降低黑高，也可以减少调整的次数。

插入元素

红黑树的概念理解起来较为复杂，我们以一个简单的示例，看看如何构造一棵红黑树。

现有数组 int[] a = {1, 10, 9, 2, 3, 8, 7, 4, 5, 6}; 我们要将其变为一棵红黑树。

首先插入1，此时树是空的，1就是根结点，根结点是黑色的：

然后插入元素10，此时依然符合规则，结果如下：

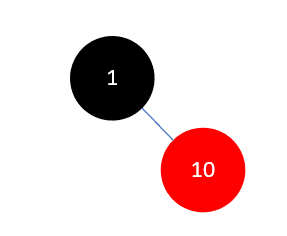
当插入元素9时，这时是需要调整的第一种情况，结果如下：

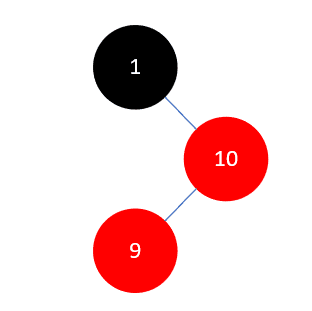
红黑树规则4中强调不能有两个相邻的红色结点，所以此时我们需要对其进行调整。调整的原则有多个相关因素，这里的情况是，父结点10是其祖父结点1（父结点的父结点）的右孩子，当前结点9是其父结点10的左孩子，且没有叔叔结点（父结点的兄弟结点），此时需要进行两次旋转，第一次，以父结点10右旋：

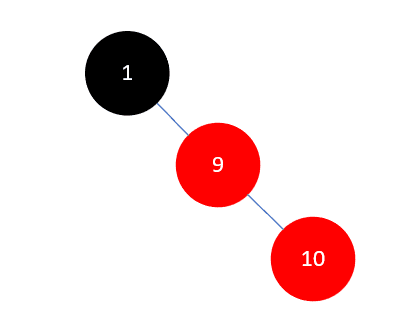
然后将父结点（此时是9）染为黑色，祖父结点1染为红色，如下所示：

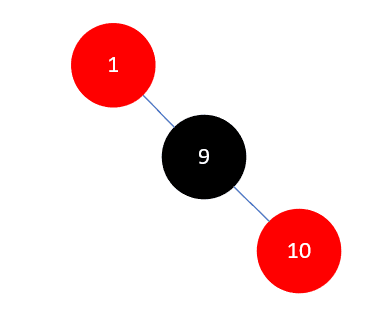
然后以祖父结点1左旋：

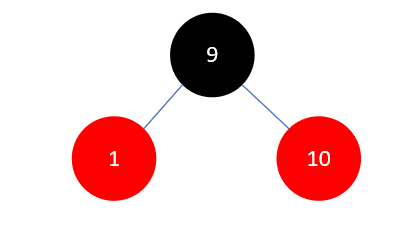
下一步，插入元素2，结果如下：

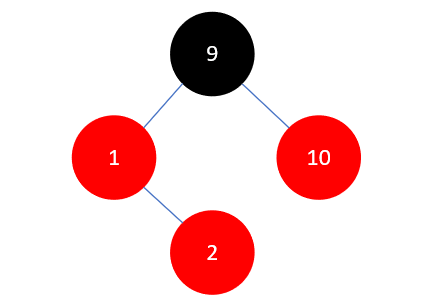
此时情况与上一步类似，区别在于父结点1是祖父结点9的左孩子，当前结点2是父结点的右孩子，且叔叔结点10是红色的。这时需要先将叔叔结点10染为黑色，再进行下一步操作，具体做法是将父结点1和叔叔结点10染为黑色，祖父结点9染为红色，如下所示：

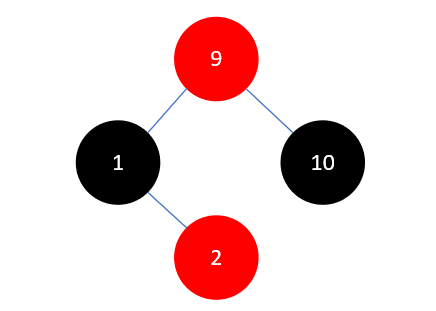
由于结点9是根节点，必须为黑色，将它染为黑色即可：

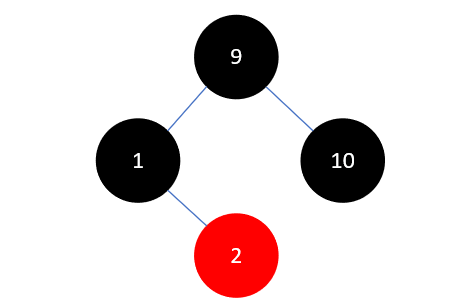
下一步，插入元素3，如下所示：

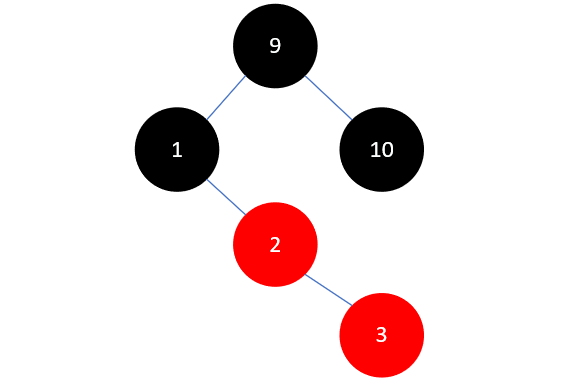
这和我们之前插入元素10的情况一模一样，需要将父结点2染为黑色，祖父结点1染为红色，如下所示：

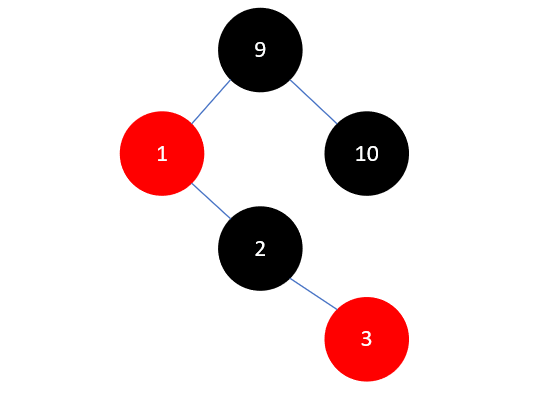
然后左旋：

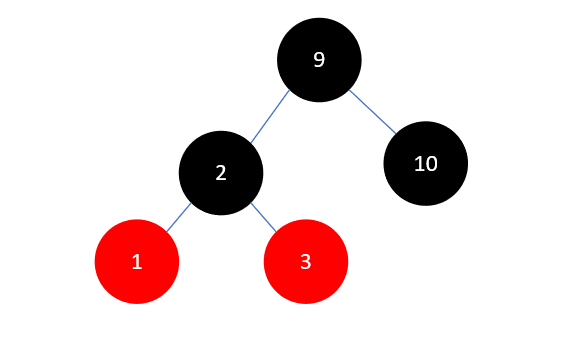
下一步，插入元素8，结果如下：

此时和插入元素2有些类似，区别在于父结点3是右孩子，当前结点8也是右孩子，这时也需要先将叔叔结点1染为黑色，具体操作是先将1和3染为黑色，再将祖父结点2染为红色，如下所示：

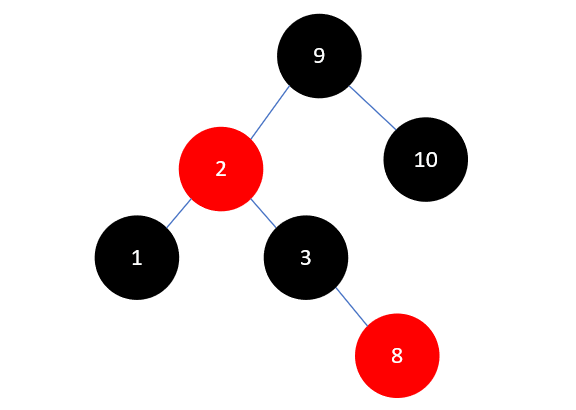
此时树已经平衡了，不需要再进行其他操作了，现在插入元素7，如下所示：

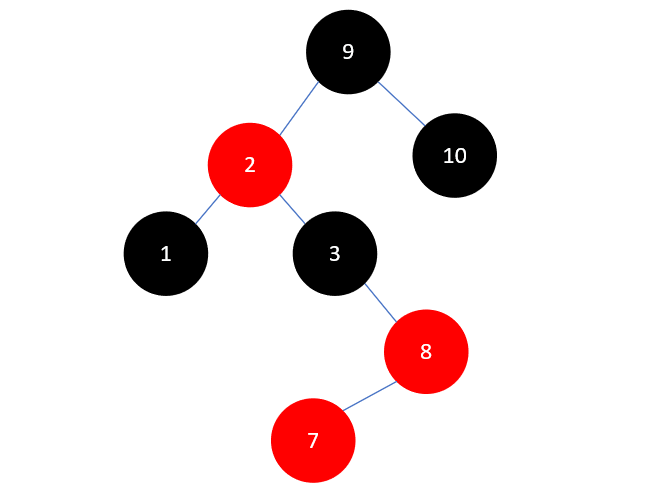
这时和之前插入元素9时一模一样了，先将7和8右旋，如下所示：

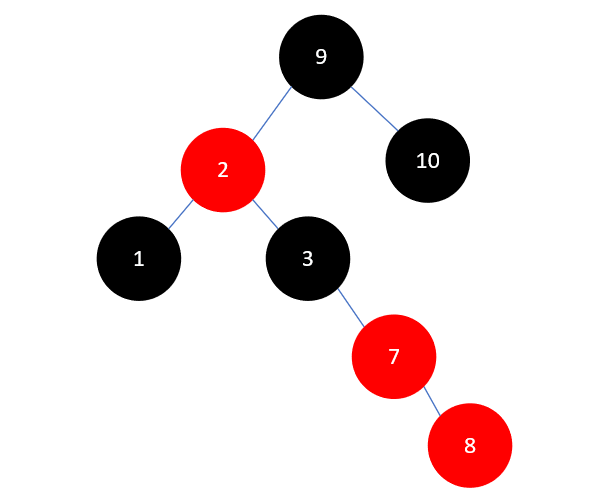
然后将7染为黑色，3染为红色，再进行左旋，结果如下：

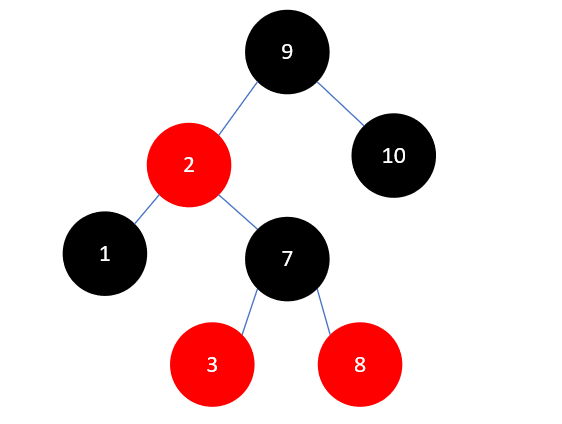
下一步要插入的元素是4，结果如下：

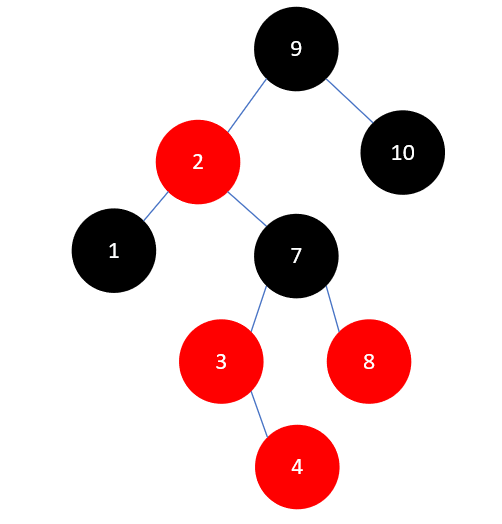
这里和插入元素2是类似的，先将3和8染为黑色，7染为红色，如下所示：

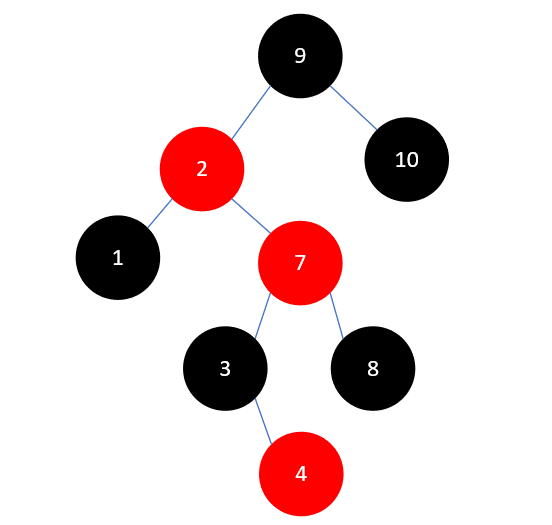
但此时2和7相邻且颜色均为红色，我们需要对它们继续进行调整。这时情况变为了父结点2为红色，叔叔结点10为黑色，且2为左孩子，7为右孩子，这时需要以2左旋。这时左旋与之前不同的地方在于结点7旋转完成后将有三个孩子，结果类似于下图：

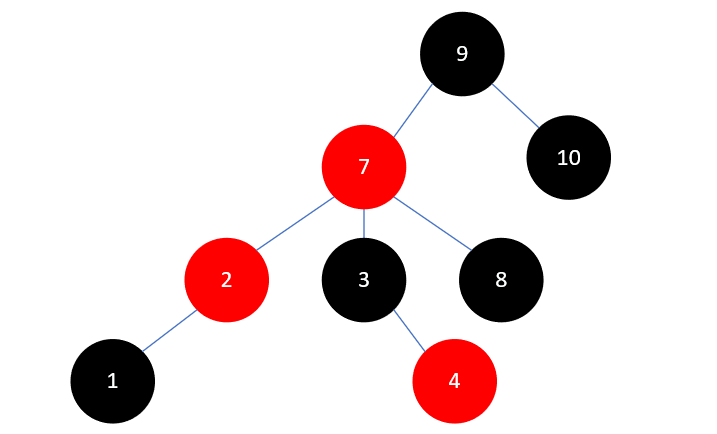
这种情况处理起来也很简单，只需要把7原来的左孩子3，变成2的右孩子即可，结果如下：

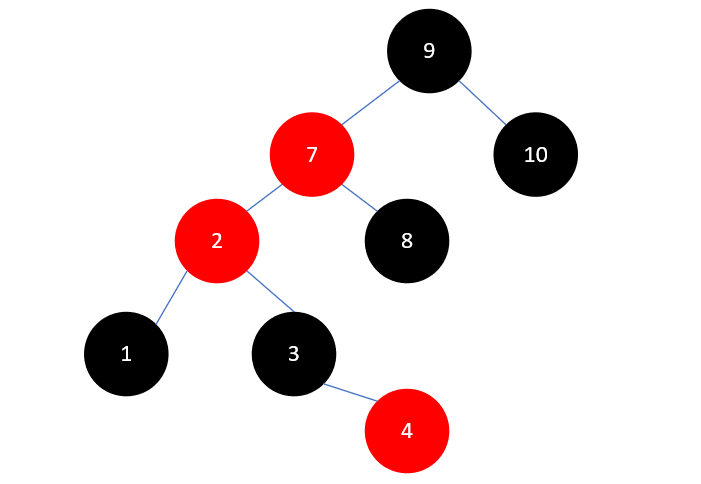
然后再把2的父结点7染为黑色，祖父结点9染为红色。结果如下所示：

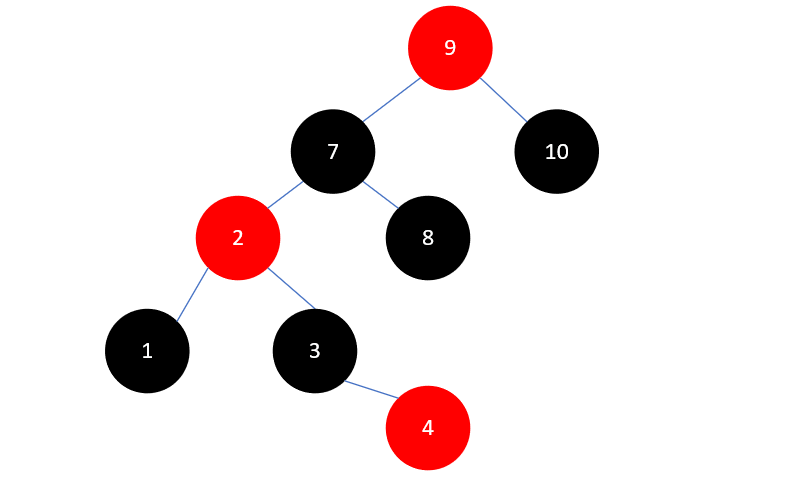
此时又需要右旋了，我们要以9右旋，右旋完成后7又有三个孩子，这种情况和上述是对称的，我们把7原有的右孩子8，变成9的左孩子即可，如下所示：

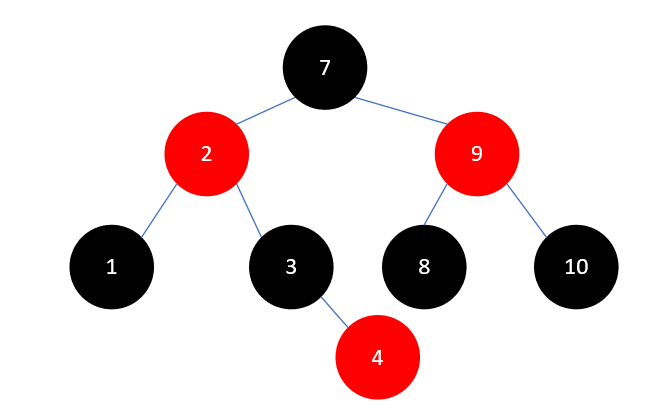
下一个要插入的元素是5，插入后如下所示：

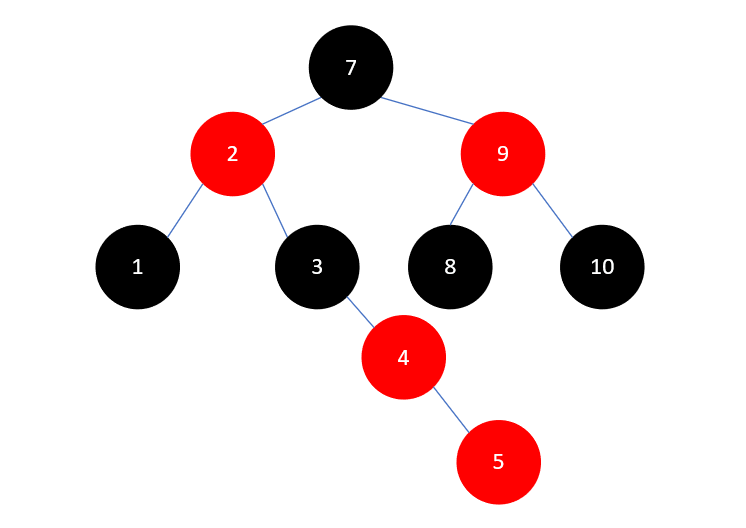
有了上述一些操作，处理5变得十分简单，将3染为红色，4染为黑色，然后左旋，结果如下所示：

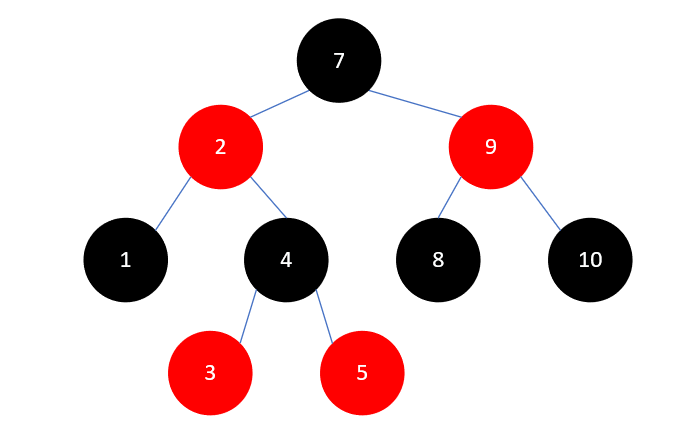
最后插入元素6，如下所示：

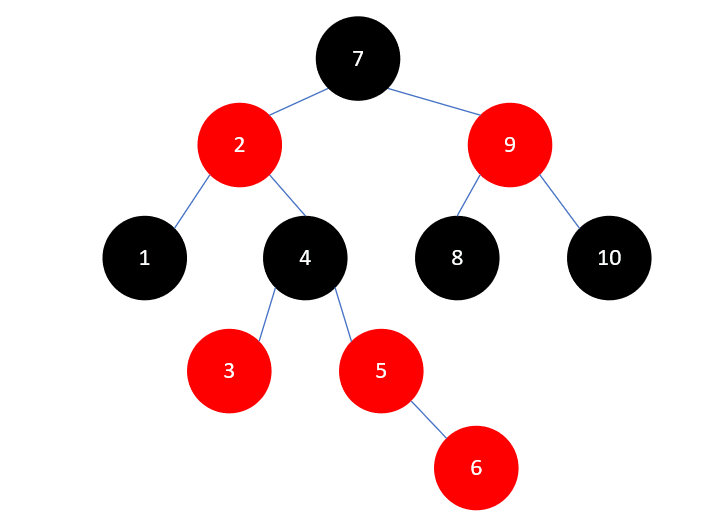
又是叔叔结点3为红色的情况，这种情况我们处理过多次了，首先将3和5染为黑色，4染为红色，结果如下：

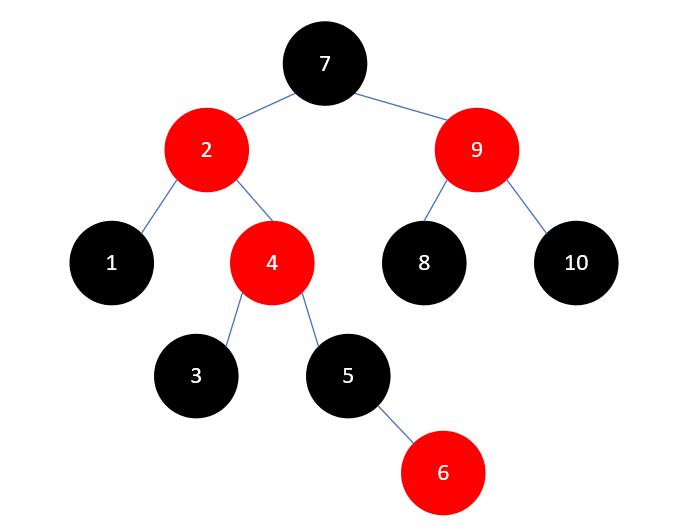
此时问题向上传递到了元素4，我们看2、4、7、9的颜色和位置关系，这种情况我们也处理过，先将2和9染为黑色，7染为红色，结果如下：

最后7是根结点，染为黑色即可，最终结果如下所示：

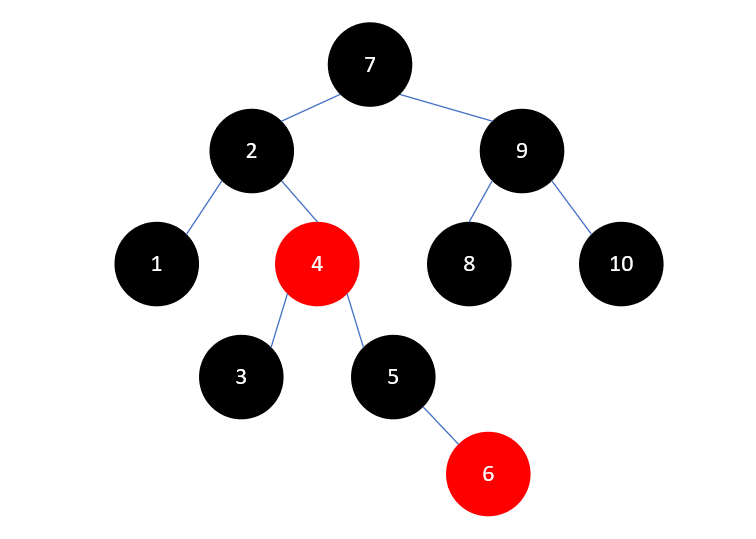
插入总结

可以看到，在插入元素时，叔叔结点是主要影响因素，待插入结点与父结点的关系决定了是否需要多次旋转。可以总结为以下几种情况：

• 如果父结点是黑色，插入即可，无需调整。
• 如果叔叔结点是红色，就把父结点和叔叔结点都转为黑色，祖父结点转为红色，将不平衡向上传递。
• 如果叔叔结点是黑色或者没有叔叔结点，就看父结点和待插入结点的关系。如果待插入结点和父结点的关系，与父结点与祖父结点的关系一致，比如待插入结点是父结点的左孩子，父结点也是祖父结点的左孩子，就无需多次旋转。否则就先通过相应的旋转将其关系变为一致。

删除元素

要从一棵红黑树中删除一个元素，主要分为三种情况。

情况-1：待删除元素没有孩子

没有孩子指的是没有值不为NIL的孩子。这种情况下，如果删除的元素是红色的，可以直接删除，如果删除的元素是黑色的，就需要进行调整了。

例如我们从下图中删除元素1：

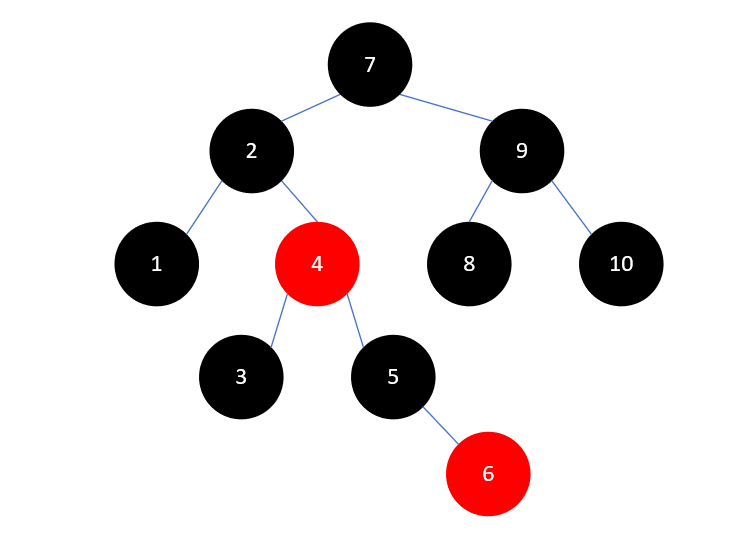
删除元素1后，2的左孩子为NIL，这条支路上的黑色结点数就比其他支路少了，所以需要进行调整。

这时，我们的关注点从叔叔结点转到兄弟结点，也就是结点4，此时4是红色的，就把它染为黑色，把父结点2染为红色，如下所示：

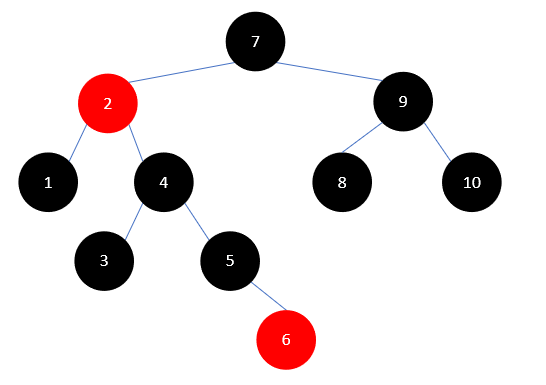
然后以2左旋，结果如下：

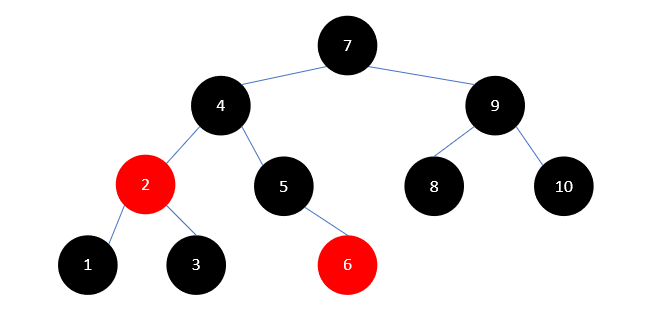
此时兄弟结点为3，且它没有红色的孩子，这时只需要把它染为红色，父结点2染为黑色即可。结果如下所示：

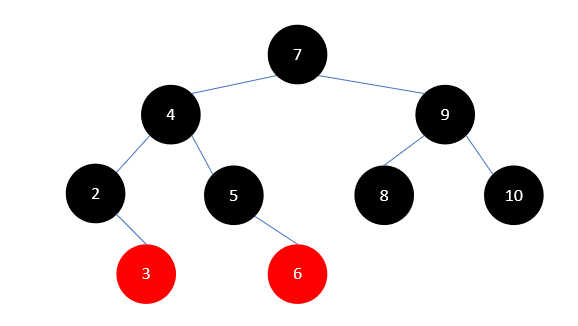
情况-2：待删除元素有一个孩子

这应该是删除操作中最简单的一种情况了，根据红黑树的定义，我们可以推测，如果一个元素仅有一个孩子，那么这个元素一定是黑色的，而且其孩子是红色的。

假设我们有一个红色节点，它是树中的某一个节点，且仅有一个孩子，那么根据红色节点不能相邻的条件，它的孩子一定是黑色的，如下所示：

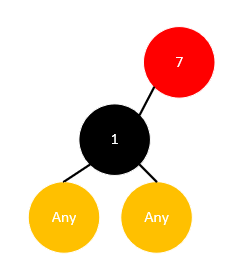
但这个子树的黑高却不再平衡了（注意每个节点的叶节点都是一个NIL节点），因此红色节点不可能只有一个孩子。

而若是一个黑色节点仅有一个孩子，如果其孩子是黑色的，同样会打破黑高的平衡，所以其孩子只能是红色的，如下所示：

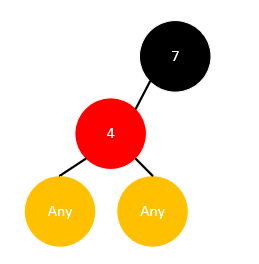
只有这一种情况符合红黑树的定义，这时要删除这个元素，只需要使用其孩子代替它，仅代替值而不代替颜色即可，上图的情况删除完后变为：

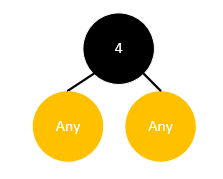
可以看到，树的黑高并没有发生变化，因此也不需要进行调整。

情况-3：待删除元素有两个孩子

我们在讨论二叉排序树时说过，如果删除一个有两个孩子的元素，可以使用它的前驱或者后继结点代替它。因为它的前驱或者后继结点最多只会有一个孩子，所以这种情况可以转为情况1或情况2处理。

删除总结

删除元素最复杂的是情况1，这主要由其兄弟结点以及兄弟结点的孩子颜色共同决定。这里简要做下总结。

我们以N代表当前待删除节点，以P代表父结点，以S代表兄弟结点，以SL代表兄弟结点的左孩子，SR代表兄弟结点的右孩子，如下所示：

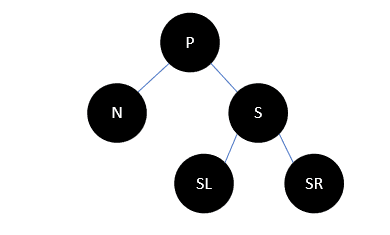
根据红黑树定义，这种情况下S要么有红色的子结点，要么只有NIL结点，以下对S有黑色结点的情况均表示NIL。

主要有以下几种：

1. S是红色，P一定是黑色，S也不会有红色的孩子，如下：

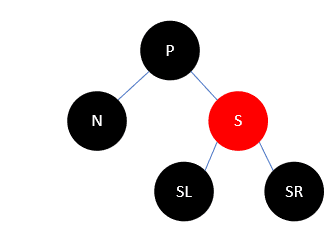
此时把P和S颜色变换，再左旋，如下：

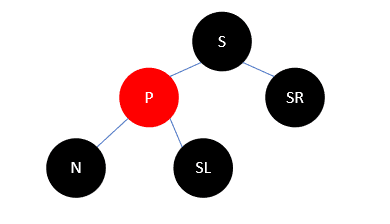
这样变换后，N支路上的黑色结点并没有增加，所以依然少一个，

2. P，S以及S的全部孩子都是黑色。

无论S有几个孩子，或者没有孩子，只要不是红色都是这种情况，此时情况如下：

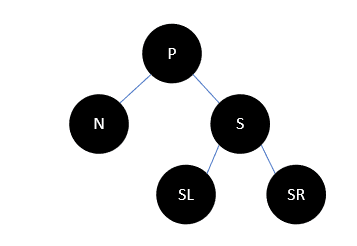
我们把S染为红色，这样一来，N和S两个支路都少了一个黑色结点，所以可以把问题向父结点转移，通过递归解决。染色后如下：

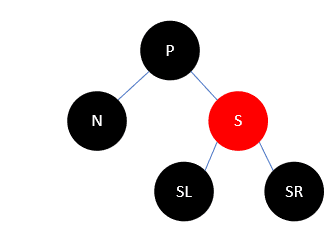
3. P为红（S一定为黑），S的孩子都为黑。

这种情况最为简单，只需要把P和S颜色交换即可。这样N支路多了一个黑色元素，而S支路没有减少，所以达到了平衡。

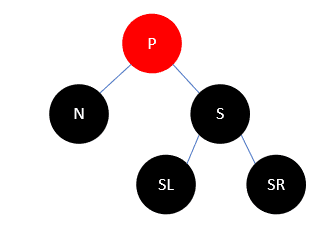
4. P任意色，S为黑，N是P的左孩子，S的右孩子SR为红，S的左孩子任意。

如下所示：

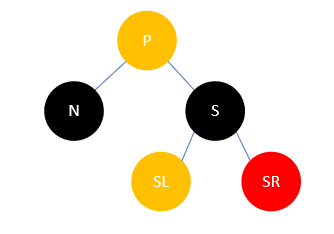
此时将S改为P的颜色，SR和P改为黑色，然后左旋，结果如下：

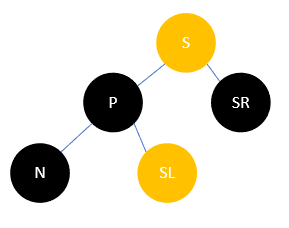
可以发现，此时N支路多了一个黑色结点，而其余支路均没有收到影响，所以调整完毕。

5. P任意色，S为黑，N是P的左孩子，S的左孩子SL为红，S的右孩子SR为黑，如下所示：

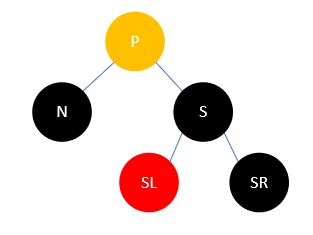
此时变换S和SL的颜色，然后右旋，结果如下：

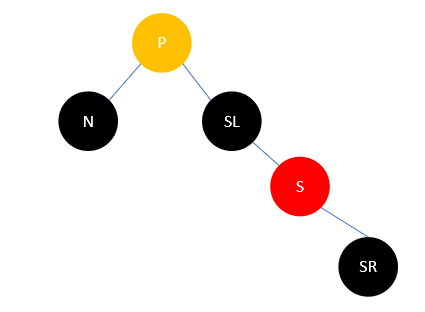
这时，所有分支的黑色结点数均没有改变，但情况5转为了情况4，再进行一次操作即可。

还有一些情况与上述是对称的，我们进行相应的转换即可。

总结

红黑树的操作比较复杂，插入元素可能需要多次变色与旋转，删除也是。这些操作的目的都是为了保证红黑树的结构不被破坏。这些复杂的插入与删除操作希望大家可以亲手尝试一下，以加深理解。

红黑树是 JDK 中 TreeMap、TreeSet 的底层数据结构，在 JDK1.8 中HashMap也用到了红黑树，所以掌握它对我们后续的分析十分重要。

• 关于红黑树与AVL树的区别？
• 为何选用红黑树？