CH15-高级同步-内存序

因果关系与顺序是非常直观的，黑客往往能比一般人更好的掌握这些概念。在编写、分析和调试使用标准互斥机制(尤其是锁)的顺序、并行代码时，这些直觉可以成为非常强大的工具。不幸的是，当面对那些并未使用标准机制的代码时这种直觉将彻底失败。一个重要的例子当然是一些代码使用了这些标准机制，但是另外一些使用了更弱的同步机制。事实上，一些人认为更弱也算是一个有点。本章将帮助你了解有效实现同步原语和性能敏感代码的内存排序。

15.1 排序：Why & How？

内存排序的一个动机可以在代码清单 15.1 中的石蕊测试中看到，咋一看似乎 exists 子句可能永远不会触发。毕竟，如果 exists 子句中的 0:r2=0，我们可以期望“线程 P0 中由 x1 加载到 r2”发生在“线程 P1 对 x1 的保存”，进一步期望“P1 中由 x0 加载到 r2”必须发生在“P0 对 x0 的保存”，因此 1:r2=2，从而不会触发 exists 子句。这个例子是对称的，因此类似的原因会让我们认为 1:r2=0 保证 0:r2=2。不幸的是，内存屏障的缺失使得这些期望破灭。即使是在相对更强排序的系统(x86)上，CPU 也有权对 P0 和 P1 中的语句进行重排序。

QQ 15.1：编译器同样能够对代码清单 15.1 中 P0 和 P1 的内存访问进行重排序，对吗？

通常来说，编译器优化比 CPU 可以执行更加广泛和深刻的重排序。但是，在这种情况下，READ_ONCE 和 WRITE_ONCE 中的易失性访问会阻止编译器重排序。而且还要做许多其他事情，因此本节中的示例将大量使用 READ_ONCE 和 WRITE_ONCE。有关 READ_ONCE 和 WRITE_ONCE 的更多细节可以参考 15.3 节。

这种重排序趋向可以使用诸如 Litmus7 之类的工具进行验证，该工具发现在我的笔记本上进行的 1 亿次实验中有 314 次反直觉排序。奇怪的是，两个加载返回值为 2 的完全合法的结果发生的概率反而较低，只有 167 次。这里的教训很清楚：增加反干涉性并不一定意味着能够降低概率！

15.1.1 为什么硬件乱序？

但是为什么第一处会发生内存乱序呢？是 CPU 自身不能追踪顺序吗？

人们期望计算机能够对事物保持追踪，而且很多人还坚持要求它们能够快速的追踪事物。然而如第 3 章中看到的那样，主存没有办法跟上 CPU 的速度，因为在从内存中读取单个变量的时间内，CPU 可以执行数百个指令。因此 CPU 引入了越来越大的缓存，如图 3.9 所示，这意味着虽然一个 CPU 对指定变量的第一次加载会导致昂贵的缓存未命中，如第 3.1.5 一节所述，随后的重复加载会因为初始化未命中会将该变量记载到该 CPU 的缓存中，因此 CPU 后续会非常快速的执行与该变量相关的操作。

然而，还需要适应从多个 CPU 到一组共享变量的频繁并发存储。在缓存一致性系统中，如果缓存包含指定变量的多个副本，则该变量的所有副本必须拥有相同的值。这对于并发加载非常有效，但对于并发存储不太友好：每个存储必须对旧值的所有副本(这是另一个缓存未命中)执行一些操作，考虑到光的有限速度和物质的原子性质，这要比性急的软件黑客预期的速度慢。

因此，CPU 配备了存储缓冲区，如图 15.1 所示。当一个 CPU 需要保存的变量 不在缓存时，新值将会被放置到 CPU 的存储缓冲区。然后 CPU 可以立即继续后续的执行，而不必等待存储对滞留在其他 CPU 缓存中的所有旧值执行操作。

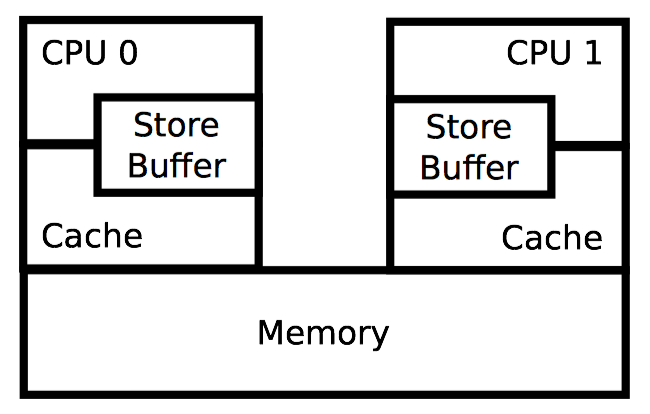
尽管存储缓冲区能够大大提升性能，但可能导致指令和内存引用无序执行，这反过来会导致严重的混淆。需要特别之处的是，这些存储缓冲区会导致内存错误排序，如清单 15.1 中 store-buffering 石蕊测试所示。

表 15.1 展示了内存乱序是如何发生的。第一行是初始状态，这时 CPU0 的缓存中持有 x1、CPU1 的缓存中持有 x0，两个变量的值均为 0。第二行展示了基于 CPU 存储的状态变化(即代码清单 15.1 中的第 9~18 行)。因为两个 CPU 在缓存中都没有要保存的变量，因此两个 CPU 都将他们的存储记录在自己的存储缓冲区中。

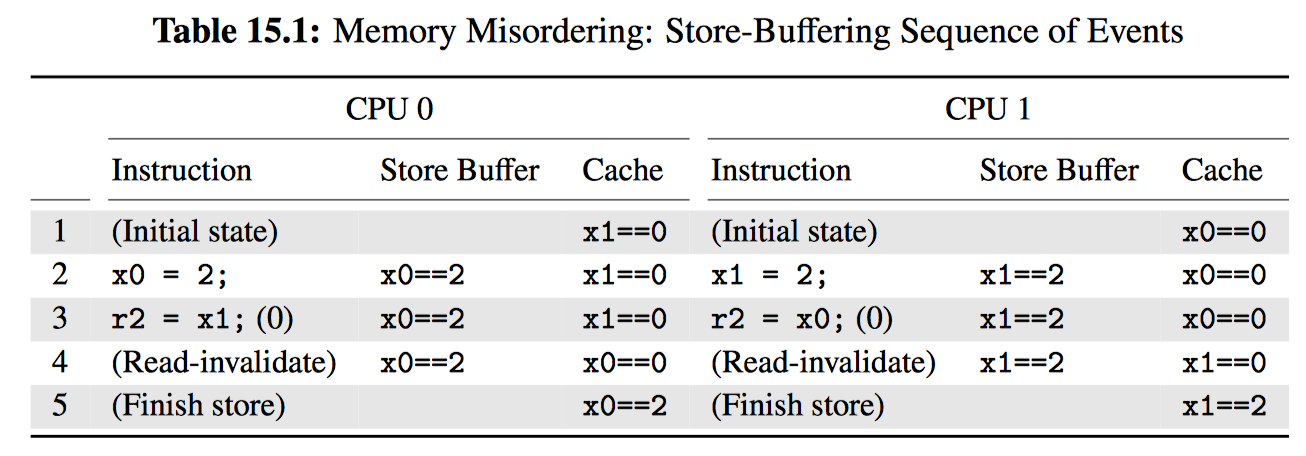
第 3 行展示了两个加载(即代码清单 15.1 中的第 1~19 行)。因为变量已被 CPU 的各自缓存加载，因此加载操作会立即返回已缓存的值，这里都是 0。

但是 CPU 还没有完成：稍后会清空自己的存储缓冲区。因为缓存在名为缓存行的较大的块中移动数据，并且因为每个缓存行可以保存多个变量，因此每个 CPU 必须将缓存行放入自己的缓存中，以便它可以更新与其存储器中的变量对应的缓存行部分，但不会影响缓存行的任何其他部分。每个 CPU 还必须确保缓存行不存在于任何其他 CPU 的缓存中，因此使用了“读无效”操作。如第 4 行所示，在两个“读无效”操作完成之后，两个 CPU 都交换了缓存行，因此 CPU0 的缓存现在包含 x0，而 CPU1 的缓存现在包含 x1。一旦两个变量出现在他们的新家中，每个 CPU 都可以将其存储缓冲区放入对应的缓存行中，使每个变量的最终值如第 5 行所示。

QQ 15.3: 但是这些值不需要由缓存被刷新到主存吗？

令人惊讶的是并不必要！在某些系统上，如果两个变量被大量使用，它们可能会在 CPU 之间来回反弹，而不会落到主存中。

总之，需要存储缓冲区来支持 CPU 高效的处理存储指令，但是可能会导致反直觉的存储器乱序。

但是如果你的算法真的需要有序的内存引用，又该怎么办呢？比如，你正在使用一对标志位来与驱动程序通信，其中一个标志表示驱动程序是否正在运行，另一个标志表示是否存在针对该驱动程序的待处理请求。请求者需要设置请求挂起的标志，然后检查驱动程序运行状态的标志，如果为 false 则唤醒驱动程序。一旦驱动程序开始为所有待处理的请求提供服务，就需要清除待处理请求的标志，然后检查请求挂起标志以查看是否需要重新启动。除非有某种办法可以确保硬件按顺序处理存储和加载，否则这种看起来非常合理的方式将无法工作。这也就是下一节的主题。

15.1.2 如何强制排序

事实上，存在编译器指令和标准同步原语(比如锁和 RCU)，他们负责通过使用内存屏障(比如 Linux 内核中的 smp_mb)来维护排序错觉。这些内存屏障可以是显式指令，比如在 ARM、POWER、Itanium、Alpha 系统上；或者由其他指令暗含，通常在 X86 系统中既是如此。因为这些标准同步原语维护了排序错觉，从而让你能够以最小的阻力使用这些原语，这样你就可以不用阅读本章的内容了。

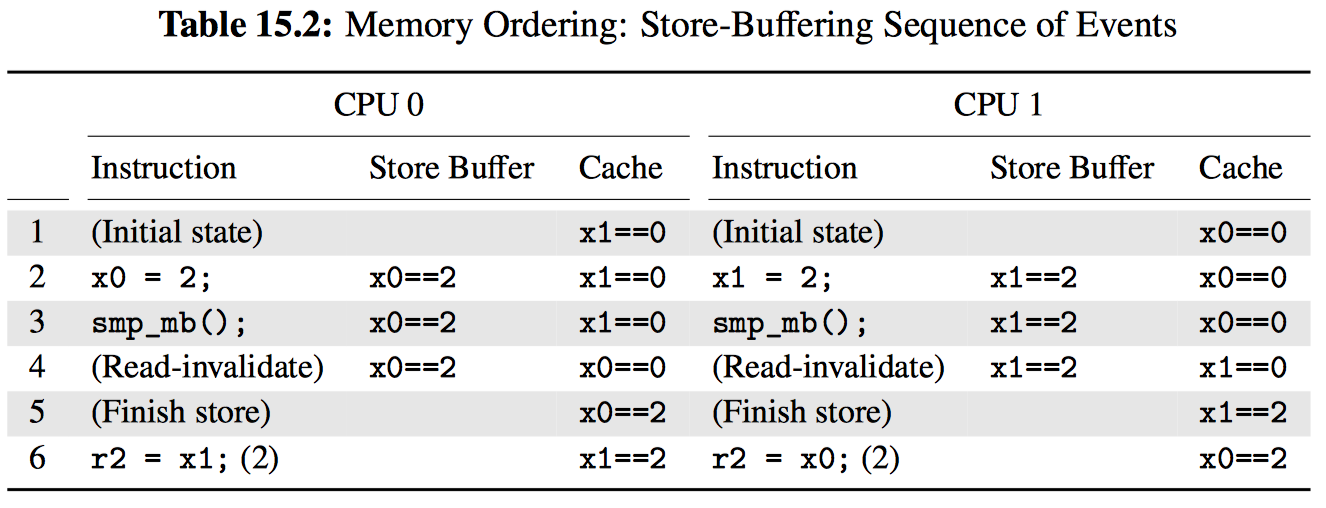
然而，如果你需要实现自己的同步原语，或者仅仅是想了解内存排序是如何工作的，那么请继续阅读！第一站是代码清单 15.2，这里将 Linux 内核的完整内存屏障 smp_mb 分别放置到 P0 和 P1 的存储和加载操作之间，其他部分则与代码清单 15.1 保持相同。这些屏障阻止了我的 X86 电脑上 1 亿次实现的反直觉结果的出现。有趣的是，由于这些屏障增加的开销导致结果合法，其中两个负载的返回值都超过 80 万次，而代码清单 15.1 中的无屏障代码仅有 167 次。

这些屏障对排序产生了深远的影响，如表 15.2 所示。虽然前两行与表 15.1 相同，同时第 3 行的 smp_mb 也不会改变状态，但是它们能够确保存储在加载之前完成，这会避免代码清单 15.1 中出现的反直觉结果。请注意，变量 x0 和 x1 在第二行仍然具有多个值，但是正如前面承诺的那样，smp_mb 最终会将一切理顺。

虽然像 smp_mb 这样的完整内存屏障拥有非常强的排序保证，其强度也伴随着极高的代价。很多情况下都可以使用更弱的排序保证来处理，这些保证使用更廉价的内存排序指令，或者在某些情况下根本不适用内存排序指令。表 15.3 提供了 Linux 内核的排序原语及对应保证的清单。每行对应一个原语或原语的类别，以及是否能够提供排序保证，同时又分为 “Prior Ordered Operation” 与 “Subsequent Ordered Operation” 两列。“Y” 表示无条件提供排序保证，否则表示排序保证是部分或有条件提供。“空”则表示不提供任何排序。

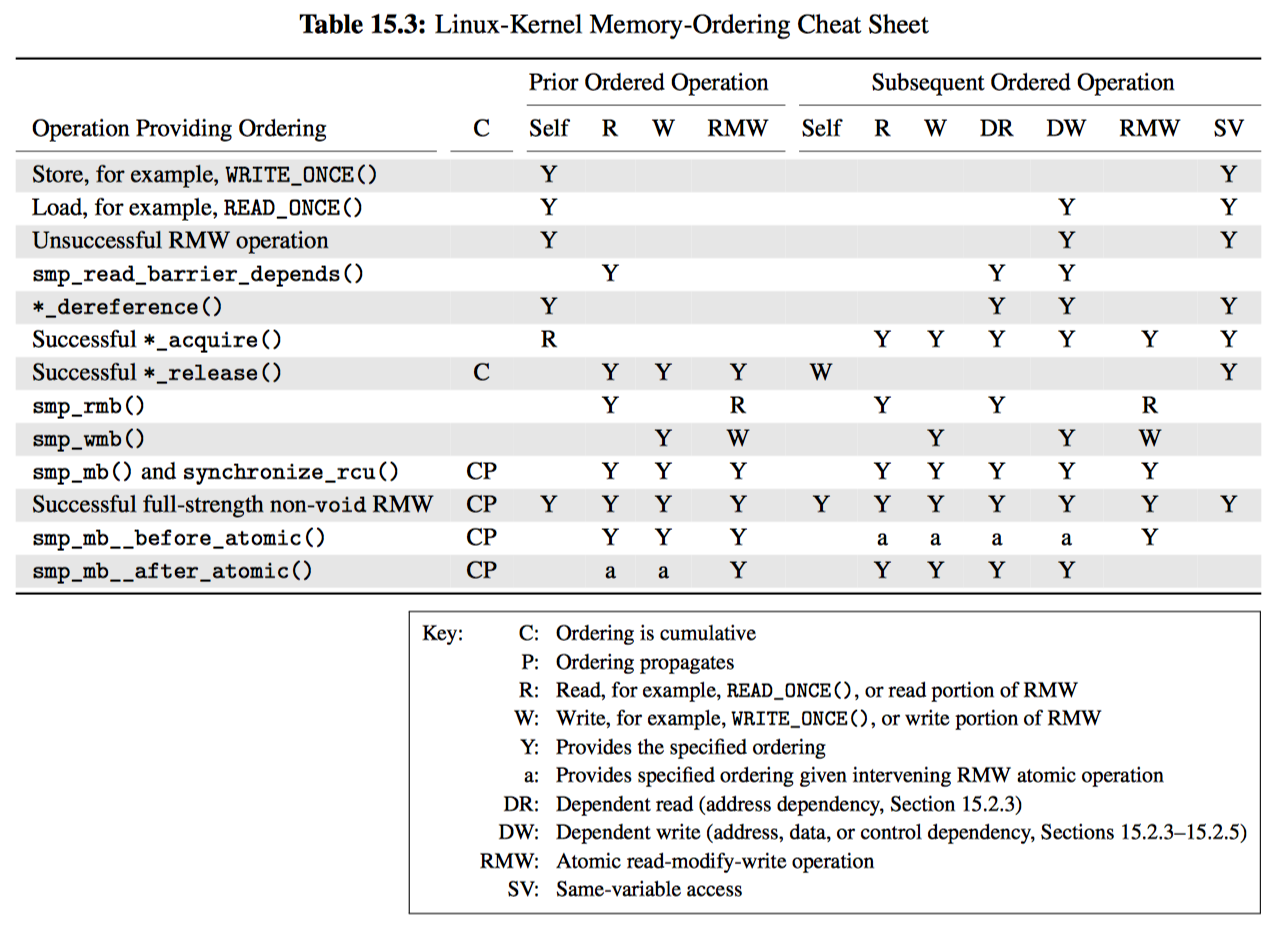
需要注意的是这只是一个速查表，因此并不能替代对内存排序的良好理解。

15.1.3 经验法则

QQ：但是我怎么知道一个给定的项目可以在这些经验法则的范围内进行设计和编码呢？

本节的内容将回答该问题。

1. 一个给定线程将按顺序看到自身的访问。
2. 排序具有条件性的 if-then 语义。
3. 排序操作必须是成对的。
4. 排序操作几乎不会提供加速效果。
5. 排序操作并非魔法。

15.2 技巧与陷阱

现在你只知道硬件可以对内存访问进行重排序，而你也可以阻止这一切的发生，下一步则是让你承认自己的自觉有问题。

首先，让我们快速了解一个变量在一个时间点可能有多少值。

15.2.1 变量带有多个值

将一个变量视为在一个定义良好的全局顺序中采用一个定义良好的值序列是很自然的。不幸的是，接下来将对这个令人欣慰的事情说再见。

考虑代码清单 15.3 中的片段。该代码又多个 CPU 并行执行。第 1 行将共享变量设置为当前 CPU 的 ID，第 2 行从 gettb 函数初始化多个变量，该函数提供在所有 CPU 之间同步的细粒度硬件“基于时间的”计数器的值。第 3~8 行的循环记录了变量保留该 CPU 分配给他的值的时间长度。当然，其中一个 CPU 将赢，因此如果不是第 6~7 行的检查，将永远不会退出循环。

退出循环后，firsttb 将保留分配后不久的时间戳，lasttb 将保持在指定值的共享变量的最后一次采样之前所采用的时间戳，或者如果共享变量已更改则保持等于在进入循环之前的 firsttb 的值。这样我们可以子啊 532ns 的时间段内绘制每个 CPU 对 state.variable 值的视图，如图 15.4 所示。

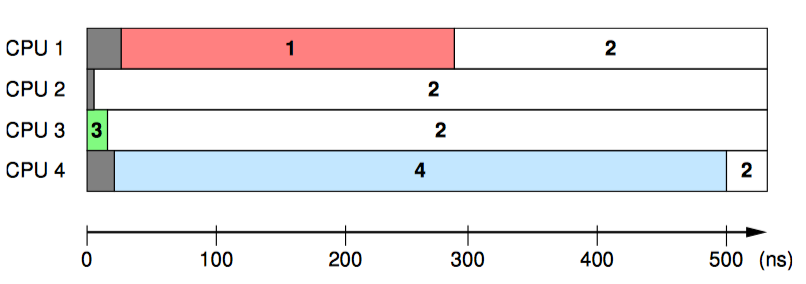
每个横轴表示指定 CPU 随时间的观察结果，左侧的灰色区域表示对应 CPU 的第一次测量之前的时间。在前 5ns 期间，只有 CPU3 对变量的值有判断。在接下来的 10ns 期间，CPU2 和 CPU3 对变量的值不一致，但此后一致认为该值为 2，这实际是最终商定的值。但是 CPU1 认为该值为 1 的持续时间长达 300ns，而 CPU4 认为该值为 4 的持续时间长达 500ns。

15.2.2 内存引用重排序

上一节表明，即使是相对强有序的系统(x86)也可能在后续的加载中重排序之前的存储，至少在存储和加载不同的变量是会发生这样的状况。本节以此结果为基础，查看加载和存储的其他组合。

15.2.2.1 加载后跟加载

代码清单 15.4 展示了经典的消息传递石蕊测试，x0 表示消息，x1 作为一个标志来表示消息是否可用。在测试中，smp_mb 强制 P0 的存储排序，但是未对加载指定排序。相对强有序的体系结构(如 x86)会强制执行排序。但是弱有序的体系结构通常不会(如 AMP+11)。因此。列表第 25 行的 exists 子句可以被触发。

从不同位置排序加载的一个基本原理是，这样做允许在较早的加载错过缓存时继续执行，但是后续加载的值已经存在。

因此，依赖于有序加载的可移植代码必须添加显式排序，比如在清单 15.5 的第 20 行添加的 smp_mb，这会组织触发 exists 子句。

15.2.2.2 加载后跟存储

代码清单 15.6 展示了经典的“加载缓冲(load-buffering)”石蕊测试。尽管相对强排序的系统(如 x86 或 IBM Mainframe)不会使用后续的存储来重排序先前的加载，但是较弱排序的系统则允许这种排序(如 AMP+11)。因此第 22 行的 exist 子句确实可能被触发。

虽然实际硬件很少展示这种重排序，但可能需要这么做的一种原因是当加载错误缓存时，存储缓冲区几乎已满，且后续存储的缓存行已准备就绪。因此，可移植代码必须强制执行任何必要的排序。比如清单 15.7 所示。smp_store_release 和 smp_load_acquire 保证第 22 行的子句永远不会触发。

15.2.2.3 存储后跟存储

代码清单 15.8 再次展示了经典的消息传递石蕊测试，其中使用 smp_mb 为 P1 的加载提供排序，但是并未给 P0 的存储提供任何排序。再次，相对强的系统架构会执行强制排序，而相对弱的系统架构则并不一定会这么做，这意味着 exists 子句可能会触发。这种重排序可能有益的一种场景是：当存储缓冲区已满，另一个存储区已准备好执行，但最旧的缓存行尚不可用。在这种情况下，允许存储无需完成将允许继续执行。因此，可移植代码必须显式的对存储进行排序，如代码清单 15.5 所示，从而防止 exists 子句的触发。

15.2.3 地址依赖

当加载指令的返回值被用于计算稍后的内存引用所要使用的地址时，产生地址依赖。

代码清单 15.9 展示了消息传递模式的一种链式变型。头指针是 x1，它最初引用 int 变量 y(第 5 行)，后者又被初始化为值 1(第 4 行)。P0 将头指针 x1 更新为引用 x0(第 12 行)，但仅将其初始化为 2(第 10 行)并强制排序(第 11 行)。P1 获取头指针 x1(第 21 行)，然后加载引用的值(第 22 行)。因此，从 21 行的加载到 22 行上的加载存在地址依赖性。在这种情况下，第 21 行返回的值恰好是第 22 行使用的地址，但是可能存在很多变化。

人们可能会期望在第 22 行的取消引用之前排序来自头指针的第 21 行的加载。但是，DEC Alpha 并不是这种做法，它可以使用相关加载的推测值，如第 15.4.1 节中更详细的描述。因此，代码清单 15.9 中的 exists 子句可以被触发。

代码清单 15.10 展示了如何使其正确的工作，即便是在 DEC Alpha 上，将第 21 行的 READ_ONCE 替换为 lockless_dereference，其作用类似于 DEC Alpha 意外所有平台上的 READ_ONCE 后跟 smp_mb，从而在所有平台上执行所需的排序，进而防止 exists 子句触发。

但是，如果依赖操作是存储而非加载又会发生什么呢，比如，在代码清单 15.11 中显示的石蕊测试。因为没有产生质量的平台推测存储，第 10 行的 WRITE_ONCE 不可能覆盖第 21 行的 WEITE_ONCE，这意味着第 25 行的 exists 子句及时在 DEC Alpha 上也无法触发，即使没有在依赖负载的情况下需要的 lockless_dereference。

然而，特别需要注意的是，地址依赖很脆弱，很容易就能被编译器优化打破。

15.2.4 数据依赖

当加载指令的返回值被用于计算稍后的存储指令要存储的数据时，则会发生数据依赖。请注意上面的“数据”：如果加载返回的值用于计算稍后的存储指令要使用的地址时，那么将是地址依赖性。

代码清单 15.12 与清单 15.7 类似，不同之处在于第 18~19 行之间的 P1 排序不是由获取加载强制执行，而是由数据依赖性完成：第 18 行加载的值是第 19 行要存储的值。这种数据依赖性提供的排序足以放置 exists 子句的触发。

和地址依赖性一样，数据依赖性也很脆弱，可以被编译器优化轻松破解。如第 15.3.2 节所述。实际上，数据依赖性可能比地址依赖性更加脆弱。原因是地址依赖性通常涉及指针值。相反，如清单 15.12 所示，通过整数值来传递数据依赖性是很诱人的，编译器可以更自由的优化不存在性。仅举一个例子，如果加载的整数乘以常数 0，编译器将知道结果为 0，因此可以用常数 0 替换加载的值，从而打破依赖性。

简而言之，你可以依赖于数据依赖性，但前提是你要注意防止编译器对他们的破坏。

15.2.5 控制依赖

当需要测试加载指令的返回值以确定是否执行稍后的存储指令时，发生控制依赖性，请注意“稍后的存储指令”：很多平台并不遵循加载到加载控制的依赖关系。

代码清单 15.13 展示了另一个加载——启动示例，这里使用的是控制依赖关系(第 19 行)来命令第 18 行的加载和第 20 行的存储。这种排序足以避免 exists 子句的触发。

但是，控制依赖性甚至比数据依赖性更易被优化掉。第 15.3.3 节描述了为了防止编译器破坏控制依赖性必须要遵循的一些规则。

值得重申的是，控制依赖性仅提供从加载到存储的排序。因此，代码清单 15.14 的第 17~19 行展示的加载到加载过程并不提供排序，因此不会阻止 exists 子句的触发。

总之，控制依赖关系可能很有用，但它们是高维护项。因此，只有在性能考虑不允许其他解决方案时才应使用。

15.2.6 缓存连贯性

在缓存一致性平台上，所有 CPU 都遵循加载到存储指定变量的顺序。幸运的是，当使用 READ_ONCE 和 WRITE_ONCE 时，几乎所有平台都是缓存一致的，如表 15.3 中所示的 SV 一列。

代码清单 15.15 展示了测试缓存连贯性的石蕊测试，其中 IRIW 代表独立写入的独立读取。因为该石蕊测试仅使用一个变量，所以 P2 和 P3 必须在 P0 和 P1 的存储顺序上达成一致。换句话说，如果 P2 认为 P0 的存储首先进行，则 P3 最好不要相信 P1 的存储首先出现。事实上，如果出现这样的情况，第 35 行的 exists 语句将被触发。

很容易推测，对于单个内存区域(比如使用 C 语言的 union 关键字设置)，不同大小的重叠加载和存储将提供类似的排序保证。然而 Flur 等人发现了一些令人惊讶的简单石蕊测试，这名这些保证可以在真实硬件上被打破。因此，至少在考虑可移植性的情况下，有必要将代码限制为对指定变量的非重叠相同大小的对齐访问。

添加更多的变量和线程会增加重排序和违反其他反直觉行文的范围，如下一节所述。

15.2.7 多重原子性

Threads running on a multicopy atomic (SF95) platform are guaranteed to agree on the order of stores, even to different variables. A useful mental model of such a system is the single-bus architecture shown in Figure 15.7. If each store resulted in a message on the bus, and if the bus could accommodate only one store at a time, then any pair of CPUs would agree on the order of all stores that they observed. Unfortunately, building a computer system as shown in the figure, without store buffers or even caches, would result in glacial computation. CPU vendors interested in providing multicopy atomicity have therefore instead provided the slightly weaker other-multicopy atomicity (ARM17, Section B2.3), which excludes the CPU doing a given store from the requirement that all CPUs agree on the order of all stores. This means that if only a subset of CPUs are doing stores, the other CPUs will agree on the order of stores, hence the “other” in “other-multicopy atomicity”. Unlike multicopy-atomic platforms, within other-multicopy-atomic platforms, the CPU doing the store is permitted to observe its store early, which allows its later loads to obtain the newly stored value directly from the store buffer. This in turn avoids abysmal performance.

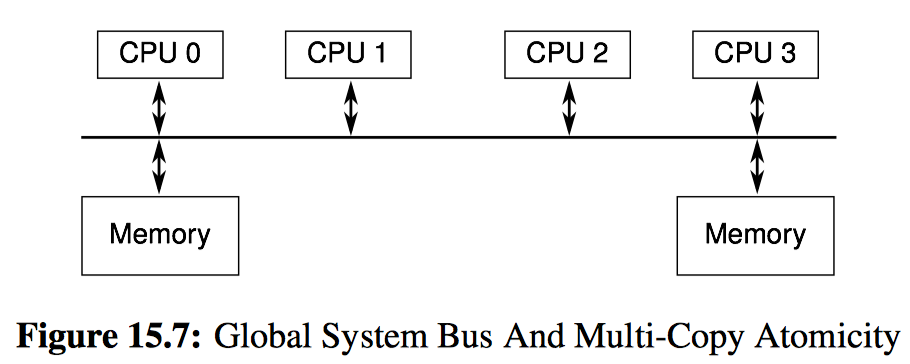
Perhaps there will come a day when all platforms provide some flavor of multicopy atomicity, but in the meantime, non-multicopy-atomic platforms do exist, and so software must deal with them.

Listing 15.16 (C-WRC+o+o-data-o+o-rmb-o.litmus) demonstrates multicopy atomicity, that is, on a multicopy-atomic platform, the exists clause on line 29 cannot trigger. In contrast, on a non-multicopy-atomic platform this exists clause can trigger, despite P1()’s accesses being ordered by a data dependency and P2()’s accesses being ordered by an smp_rmb(). Recall that the definition of multicopy atomicity requires that all threads agree on the order of stores, which can be thought of as all stores reaching all threads at the same time. Therefore, a non-multicopy-atomic platform can have a store reach different threads at different times. In particular, P0()’s store might reach P1() long before it reaches P2(), which raises the possibility that P1()’s store might reach P2() before P0()’s store does.

This leads to the question of why a real system constrained by the usual laws of physics would ever trigger the exists clause of Listing 15.16. The cartoonish diagram of a such a real system is shown in Figure 15.8. CPU 0 and CPU 1 share a store buffer, as do CPUs 2 and 3. This means that CPU 1 can load a value out of the store buffer, thus potentially immediately seeing a value stored by CPU 0. In contrast, CPUs 2 and 3 will have to wait for the corresponding cache line to carry this new value to them.

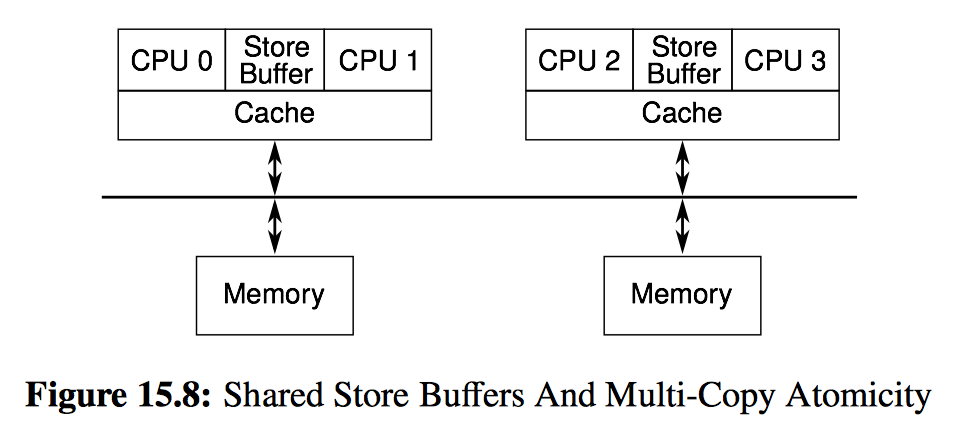
Table 15.4 shows one sequence of events that can result in the exists clause in Listing 15.16 triggering. This sequence of events will depend critically on P0() and P1() sharing both cache and a store buffer in the manner shown in Figure 15.8.

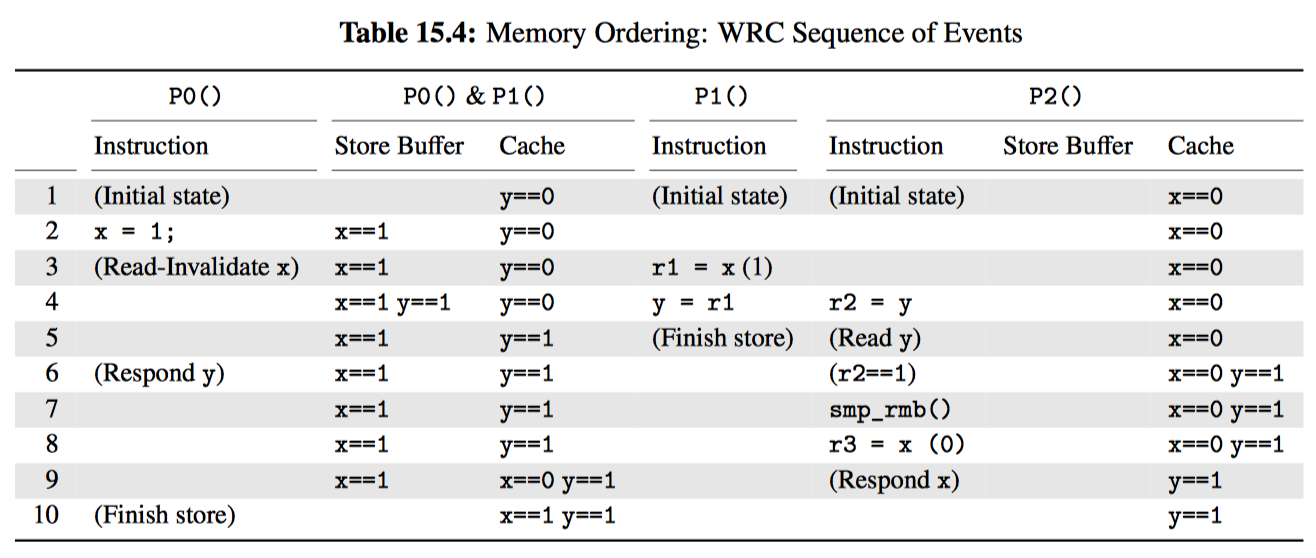
Row 1 shows the initial state, with the initial value of y in P0()’s and P1()’s shared cache, and the initial value of x in P2()’s cache.

Row 2 shows the immediate effect of P0() executing its store on line 8. Because the cacheline containing x is not in P0()’s and P1()’s shared cache, the new value (1) is stored in the shared store buffer.

Row 3 shows two transitions. First, P0() issues a read-invalidate operation to fetch the cacheline containing x so that it can flush the new value for x out of the shared store buffer. Second, P1() loads from x (line 15), an operation that completes immediately because the new value of x is immediately available from the shared store buffer.

Row 4 also shows two transitions. First, it shows the immediate effect of P1() executing its store to y (line 16), placing the new value into the shared store buffer. Second, it shows the start of P2()’s load from y (line 24).

Row 5 continues the tradition of showing two transitions. First, it shows P1() complete its store to y, flushing from the shared store buffer to the cache. Second, it shows P2() request the cacheline containing y.

Row 6 shows P2() receive the cacheline containing y, allowing it to finish its load into r2, which takes on the value 1.

Row 7 shows P2() execute its smp_rmb() (line 25), thus keeping its two loads ordered.

Row 8 shows P2() execute its load from x, which immediately returns with the value zero from P2()’s cache.

Row 9 shows P2() finally responding to P0()’s request for the cacheline containing x, which was made way back up on row 3.

Finally, row 10 shows P0() finish its store, flushing its value of x from the shared store buffer to the shared cache.

Note well that the exists clause on line 29 has triggered. The values of r1 and r2 are both the value one, and the final value of r3 the value zero. This strange result occurred because P0()’s new value of x was communicated to P1() long before it was communicated to P2().

This counter-intuitive result happens because although dependencies do provide ordering, they provide it only within the confines of their own thread. This threethread example requires stronger ordering, which is the subject of Sections 15.2.7.1 through 15.2.7.4.

15.2.7.1 Cumulativity

The three-thread example shown in Listing 15.16 requires cumulative ordering, or cumulativity. A cumulative memory-ordering operation orders not just any given access preceding it, but also earlier accesses by any thread to that same variable.

Dependencies do not provide cumulativity, which is why the “C” column is blank for both the READ_ONCE() and the smp_read_barrier_depends() rows of Table 15.3. However, as indicated by the “C” in their “C” column, release operations do provide cumulativity. Therefore, Listing 15.17 (C-WRC+o+o-r+a-o.litmus) substitutes a release operation for Listing 15.16’s data dependency. Because the release operation is cumulative, its ordering applies not only to Listing 15.17’s load from x by P1() on line 15, but also to the store to x by P0() on line 8—but only if that load returns the value stored, which matches the 1:r1=1 in the exists clause on line 28. This means that P2()’s load-acquire suffices to force the load from x on line 25 to happen after the store on line 8, so the value returned is one, which does not match 2:r3=0, which in turn prevents the exists clause from triggering.

These ordering constraints are depicted graphically in Figure 15.9. Note also that cumulativity is not limited to a single step back in time. If there was another load from x or store to x from any thread that came before the store on line 13, that prior load or store would also be ordered before the store on line 32, though only if both r1 and r2 both end up containing the address of x.

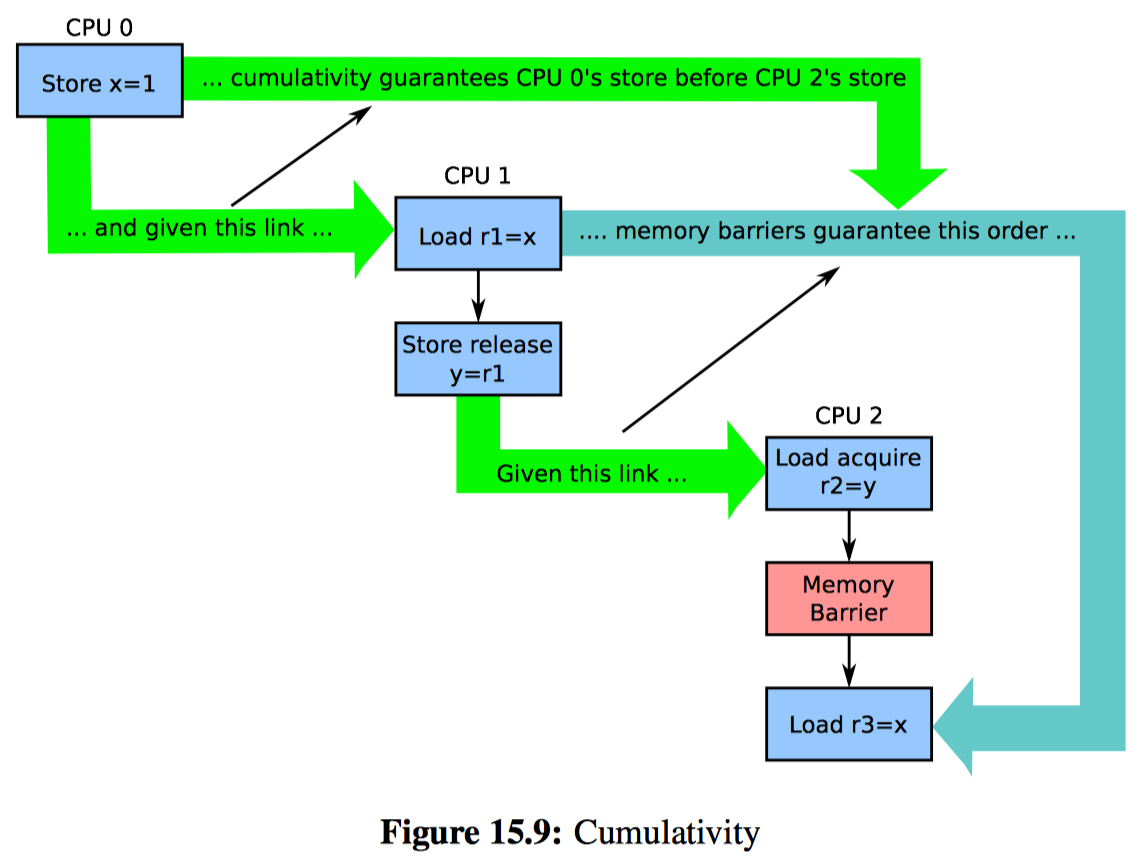
In short, use of cumulative ordering operations can suppress non-multicopy-atomic behaviors in some situations. Cumulativity nevertheless has limits, which are examined in the next section.

15.2.7.2 Propagation

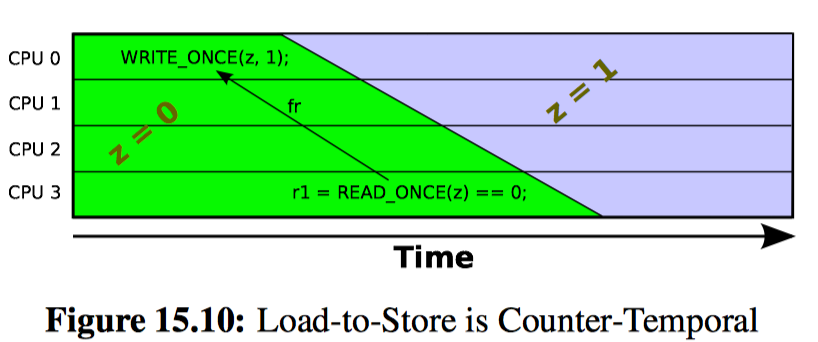
Listing 15.18 (C-W+RWC+o-r+a-o+o-mb-o.litmus) shows the limitations of cumulativity and store-release, even with a full memory barrier. The problem is that although the smp_store_release() on line 12 has cumulativity, and although that cumulativity does order P2()’s load on line 30, the smp_store_release()’s ordering cannot propagate through the combination of P1()’s load (line 21) and P2()’s store (line 28). This means that the exists clause on line 33 really can trigger.

This situation might seem completely counter-intuitive, but keep in mind that the speed of light is finite and computers are of non-zero size. It therefore takes time for the effect of the P2()’s store to z to propagate to P1(), which in turn means that it is possible that P1()’s read from z happens much later in time, but nevertheless still sees the old value of zero. This situation is depicted in Figure 15.10: Just because a load sees the old value does not mean that this load executed at an earlier time than did the store of the new value.

Note that Listing 15.18 also shows the limitations of memory-barrier pairing, given that there are not two but three processes. These more complex litmus tests can instead be said to have cycles, where memory-barrier pairing is the special case of a twothread cycle. The cycle in Listing 15.18 goes through P0() (lines 11 and 12), P1() (lines 20 and 21), P2() (lines 28, 29, and 30), and back to P0() (line 11). The exists clause delineates this cycle: the 1:r1=1 indicates that the smp_load_acquire() on line 20 returned the value stored by the smp_store_release() on line 12, the 1:r2=0 indicates that the WRITE_ONCE() on line 28 came too late to affect the value returned by the READ_ONCE() on line 21, and finally the 2:r3=0 indicates that the WRITE_ONCE() on line 11 came too late to affect the value returned by the READ_ONCE() on line 30. In this case, the fact that the exists clause can trigger means that the cycle is said to be allowed. In contrast, in cases where the exists clause cannot trigger, the cycle is said to be prohibited.

But what if we need to keep the exists clause on line 33 of Listing 15.18? One solution is to replace P0()’s smp_store_release() with an smp_mb(), which Table 15.3 shows to have not only cumulativity, but also propagation. The result is shown in Listing 15.19 (C-W+RWC+o-mb-o+a-o+o-mb-o.litmus).

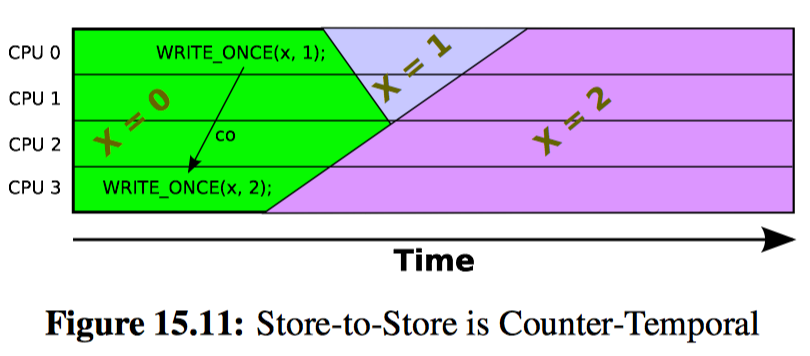
For completeness, Figure 15.11 shows that the “winning” store among a group of stores to the same variable is not necessarily the store that started last. This should not come as a surprise to anyone who carefully examined Figure 15.5.

But sometimes time really is on our side. Read on!

Happens-Before

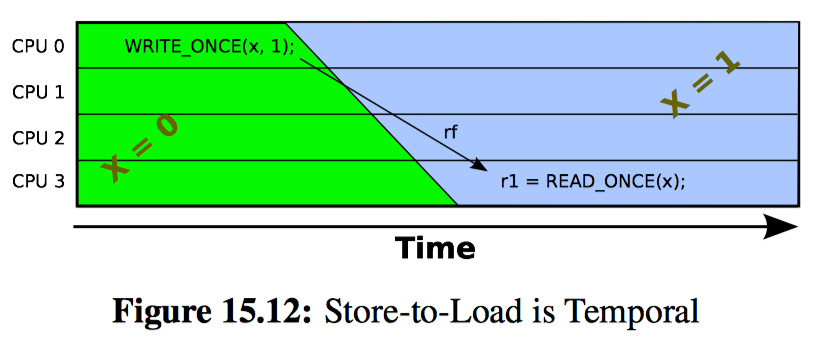
As shown in Figure 15.12, on platforms without user-visible speculation, if a load returns the value from a particular store, then, courtesy of the finite speed of light and the non-zero size of modern computing systems, the store absolutely has to have executed at an earlier time than did the load. This means that carefully constructed programs can rely on the passage of time itself as an memory-ordering operation.

Of course, just the passage of time by itself is not enough, as was seen in Listing 15.6, which has nothing but store-to-load links and, because it provides absolutely no ordering, still can trigger its exists clause. However, as long as each thread provides even the weakest possible ordering, exists clause would not be able to trigger. For example, Listing 15.21 (C-LB+a-o+o-data-o+o-data-o.litmus) shows P0() ordered with an smp_load_acquire() and both P1() and P2() ordered with data dependencies. These orderings, which are close to the top of Table 15.3, suffice to prevent the exists clause from triggering.

An important, to say nothing of more useful, use of time for ordering memory accesses is covered in the next section.

Release-Acquire Chains

A minimal release-acquire chain was shown in Listing 15.7 (C-LB+a-r+a-r+a-r+ar.litmus), but these chains can be much longer, as shown in Listing 15.22. The longer the release-acquire chain, the more ordering is gained from the passage of time, so that no matter how many threads are involved, the corresponding exists clause cannot trigger.

Although release-acquire chains are inherently store-to-load creatures, it turns out that they can tolerate one load-to-store step, despite such steps being counter-temporal, as shown in Figure 15.10. For example, Listing 15.23 (C-ISA2+o-r+a-r+a-r+ao.litmus) shows a three-step release-acquire chain, but where P3()’s final access is a READ_ONCE() from x0, which is accessed via WRITE_ONCE() by P0(), forming a non-temporal load-to-store link between these two processes. However, because P0()’s smp_store_release() (line 12) is cumulative, if P3()’s READ_ONCE() returns zero, this cumulativity will force the READ_ONCE() to be ordered before P0()’s smp_store_release(). In addition, the release-acquire chain (lines 12, 20, 21, 28, 29, and 37) forces P3()’s READ_ONCE() to be ordered after P0()’s smp_store_ release(). Because P3()’s READ_ONCE() cannot be both before and after P0()’s smp_store_release(), either or both of two things must be true:

1. P3()’s READ_ONCE() came after P0()’s WRITE_ONCE(), so that the READ_ ONCE() returned the value two, so that the exists clause’s 3:r2=0 is false.

2. The release-acquire chain did not form, that is, one or more of the exists clause’s 1:r2=2, 2:r2=2, or 3:r1=2 is false.

Either way, the exists clause cannot trigger, despite this litmus test containing a notorious load-to-store link between P3() and P0(). But never forget that releaseacquire chains can tolerate only one load-to-store link, as was seen in Listing 15.18.

Release-acquire chains can also tolerate a single store-to-store step, as shown in Listing 15.24 (C-Z6.2+o-r+a-r+a-r+a-o.litmus). As with the previous example, smp_store_release()’s cumulativity combined with the temporal nature of the release-acquire chain prevents the exists clause on line 36 from triggering. But beware: Adding a second store-to-store step would allow the correspondingly updated exists clause to trigger.

In short, properly constructed release-acquire chains form a peaceful island of intuitive bliss surrounded by a strongly counter-intuitive sea of more complex memoryordering constraints.

15.3 Compile-Time Consternation

Most languages, including C, were developed on uniprocessor systems by people with little or no parallel-programming experience. As a results, unless explicitly told otherwise, these languages assume that the current CPU is the only thing that is reading or writing memory. This in turn means that these languages’ compilers’ optimizers are ready, willing, and oh so able to make dramatic changes to the order, number, and sizes of memory references that your program executes. In fact, the reordering carried out by hardware can seem quite tame by comparison.

15.3.1 Memory-Reference Restrictions

Again, unless told otherwise, compilers assume that nothing else is affecting the variables being accessed by the generated code. This assumption is not simply some design error, but is instead enshrined in various standards. 9 This assumption means that compilers are within their rights (as defined by the standards) to optimize the following code so as to hoist the load from a out of the loop, at least in cases where the compiler can prove that do_something() does not modify a:

1 while (a) 
2 do_something();

The optimized code might look something like this, essentially fusing an arbitrarily large number of intended loads into a single actual load:

1 if (a) 
2 for (;;) 
3 	do_something();

This optimization might come as a fatal surprise to code elsewhere that expected to terminate this loop by storing a zero to a. Fortunately, there are several ways of avoiding this sort of problem:

1. Volatile accesses.
2. Atomic variables.
3. Prohibitions against introducing data races.

The volatile restrictions are necessary to write reliable device drivers, and the atomic variables and prohibitions against introducing data races are necessary to write reliable concurrent code.

Starting with volatile accesses, the following code relies on the volatile casts in READ_ONCE() to prevent the unfortunate infinite-loop optimization:

1 while (READ_ONCE(a)) 
2 	do_something();

READ_ONCE() marks the load with a volatile cast. Now volatile was originally designed for accessing memory-mapped I/O (MMIO) registers, which are accessed using the same load and store instructions that are used when accessing normal memory. However, MMIO registers need not act at all like normal memory. Storing a value to an MMIO register does not necessarily mean that a subsequent load from that register will return the value stored. Loading from an MMIO register might well have side effects, for example, changing the device state or affecting the response to subsequent loads and stores involving other MMIO registers. Loads and stores of different sizes to the same MMIO address might well have different effects.

This means that, even on a uniprocessor system, changing the order, number, or size of MMIO accesses is strictly forbidden. And this is exactly the purpose of the C-language volatile keyword, to constrain the compiler so as to allow implementation of reliable device drivers.

This is why READ_ONCE() prevents the destructive hoisting of the load from a out of the loop: Doing so changes the number of volatile loads from a, so this optimization is disallowed. However, note well that volatile does absolutely nothing to constrain the hardware. Therefore, if the code following the loop needs to see the result of any memory references preceding the store of zero that terminated the loop, you will instead need to use something like smp_store_release() to store the zero and smp_load_ acquire() in the loop condition. But if all you need is to reliably control the loop without any other ordering, READ_ONCE() can do the job.

Compilers can also replicate loads. For example, consider this all-too-real code fragment:

1 tmp = p; 
2 if (tmp != NULL && tmp <= q) 
3 	do_something(tmp);

Here the intent is that the do_something() function is never passed a NULL pointer or a pointer that is greater than q. However, the compiler is within its rights to transform this into the following:

1 if (p != NULL && p <= q) 
2 	do_something(p);

In this transformed code, the value of p is loaded three separate times. This transformation might seem silly at first glance, but it is quite useful when the surrounding code has consumed all of the machine registers. It is possible that the current value of p passes the test on line 1, but that some other thread stores NULL to p before line 2 executes, and the resulting NULL pointer could be a fatal surprise to do_something(). 10 To prevent the compiler from replicating the load, use READ_ONCE(), for example as follows:

1 tmp = READ_ONCE(p); 
2 if (tmp != NULL && tmp <= q) 
3 	do_something(tmp);

Alternatively, the variable p could be declared volatile.

Compilers can also fuse stores. The most infamous example is probably the progressbar example shown below:

1 while (!am_done()) { 
2 	do_something(p); 
3 	progress++; 
4 }

If the compiler used a feedback-driven optimizer, it might well notice that the store to the shared variable progress was quite expensive, resulting in the following well-intentioned optimization:

1 while (!am_done()) { 
2 	do_something(p); 
3 	tmp++; 
4 } 
5 progress = tmp;

This might well slightly increase performance, but the poor user watching the progress bar might be forgiven for harboring significant ill will towards this particular optimization. The progress bar will after all be stuck at zero for a long time, then jump at the very end. The following code will usually prevent this problem:

1 while (!am_done()) { 
2 	do_something(p); 
3 	WRITE_ONCE(progress, progress + 1); 
4 }

Exceptions can occur if the compiler is able to analyze do_something() and learn that it has no accesses to atomic or volatile variables. In these cases the compiler could produce two loops, one invoking do_something() and the other incrementing progress. It may be necessary to replace the WRITE_ONCE() with something like smp_store_release() in the unlikely event that this occurs. It is important to note that although the compiler is forbidden from changing the number, size, or order of volatile accesses, it is perfectly within its rights to reorder normal accesses with unrelated volatile accesses.

Oddly enough, the compiler is within its rights to use a variable as temporary storage just before a normal store to that variable, thus inventing stores to that variable. Fortunately, most compilers avoid this sort of thing, at least outside of stack variables. In any case, using WRITE_ONCE(), declaring the variable volatile, or declaring the variable atomic (in recent C and C++ compilers supporting atomics) will prevent this sort of thing.

The previous examples involved compiler optimizations that changed the number of accesses. Now, it might seem that preventing the compiler from changing the order of accesses is an act of futility, given that the underlying hardware is free to reorder them. However, modern machines have exact exceptions and exact interrupts, meaning that any interrupt or exception will appear to have happened at a specific place in the instruction stream, so that the handler will see the effect of all prior instructions, but won’t see the effect of any subsequent instructions. READ_ONCE() and WRITE_ONCE() can therefore be used to control communication between interrupted code and interrupt handlers. 11

This leaves changes to the size of accesses, which is known as load tearing and store tearing when the actual size is smaller than desired. For example, storing the constant 0x00010002 into a 32-bit variable might seem quite safe. However, there are CPUs that can store small immediate values directly into memory, and on such CPUs, the compiler can be expected to split this into two 16-bit stores in order to avoid the overhead of explicitly forming the 32-bit constant. This could come as a fatal surprise to another thread concurrently loading from this variable, which might not expect to see the result of a half-completed store. Use of READ_ONCE() and WRITE_ONCE() prevent the compiler from engaging in load tearing and store tearing, respectively.

In short, use of READ_ONCE(), WRITE_ONCE(), and volatile are valuable tools in preventing the compiler from optimizing your parallel algorithm out of existence. Compilers are starting to provide other mechanisms for avoiding load and store tearing, for example, memory_order_relaxed atomic loads and stores, however, volatile is still needed to avoid fusing and splitting of accesses.

Please note that, it is possible to overdo use of READ_ONCE() and WRITE_ONCE(). For example, if you have prevented a given variable from changing (perhaps by holding the lock guarding all updates to that variable), there is no point in using READ_ONCE(). Similarly, if you have prevented any other CPUs or threads from reading a given variable (perhaps because you are initializing that variable before any other CPU or thread has access to it), there is no point in using WRITE_ONCE(). However, in my experience, developers need to use things like READ_ONCE() and WRITE_ONCE() more often than they think that they do, the overhead of unnecessary uses is quite low. Furthermore, the penalty for failing to use them when needed is quite high.

15.3.2 Address- and Data-Dependency Difficulties

Compilers do not understand either address or data dependencies, although there are efforts underway to teach them, or at the very least, standardize the process of teaching them (MWB + 17, MRP + 17). In the meantime, it is necessary to be very careful in order to prevent your compiler from breaking your dependencies.

15.3.2.1 Give your dependency chain a good start

The load that heads your dependency chain must use proper ordering, for example, lockless_dereference(), rcu_dereference(), or a READ_ONCE() followed by smp_read_barrier_depends(). Failure to follow this rule can have serious side effects:

1. On DEC Alpha, a dependent load might not be ordered with the load heading the dependency chain, as described in Section 15.4.1.

2. If the load heading the dependency chain is a C11 non-volatile memory_order_ relaxed load, the compiler could omit the load, for example, by using a value that it loaded in the past.

3. If the load heading the dependency chain is a plain load, the compiler can omit the load, again by using a value that it loaded in the past. Worse yet, it could load twice instead of once, so that different parts of your code use different values—and compilers really do this, especially when under register pressure.

4. The value loaded by the head of the dependency chain must be a pointer. In theory, yes, you could load an integer, perhaps to use it as an array index. In practice, the compiler knows too much about integers, and thus has way too many opportunities to break your dependency chain (MWB + 17).

15.3.2.2 Avoid arithmetic dependency breakage

Although it is just fine to do some arithmetic operations on a pointer in your dependency chain, you need to be careful to avoid giving the compiler too much information. After all, if the compiler learns enough to determine the exact value of the pointer, it can use that exact value instead of the pointer itself. As soon as the compiler does that, the dependency is broken and all ordering is lost.

1. Although it is permissible to compute offsets from a pointer, these offsets must not result in total cancellation. For example, given a char pointer cp, cp-(uintptr_ t)cp) will cancel and can allow the compiler to break your dependency chain.

On the other hand, canceling offset values with each other is perfectly safe and legal. For example, if a and b are equal, cp+a-b is an identity function, including preserving the dependency.

2. Comparisons can break dependencies. Listing 15.26 shows how this can happen. Here global pointer gp points to a dynamically allocated integer, but if memory is low, it might instead point to the reserve_int variable. This reserve_ int case might need special handling, as shown on lines 6 and 7 of the listing. But the compiler could reasonably transform this code into the form shown in Listing 15.27, especially on systems where instructions with absolute addresses run faster than instructions using addresses supplied in registers. However, there is clearly no ordering between the pointer load on line 5 and the dereference on line 8. Please note that this is simply an example: There are a great many other ways to break dependency chains with comparisons.

Note that a series of inequality comparisons might, when taken together, give the compiler enough information to determine the exact value of the pointer, at which point the dependency is broken. Furthermore, the compiler might be able to combine information from even a single inequality comparison with other information to learn the exact value, again breaking the dependency. Pointers to elements in arrays are especially susceptible to this latter form of dependency breakage.

15.3.2.3 Safe comparison of dependent pointers

It turns out that there are several safe ways to compare dependent pointers:

1. Comparisons against the NULL pointer. In this case, all the compiler can learn is that the pointer is NULL, in which case you are not allowed to dereference it anyway.

2. The dependent pointer is never dereferenced, whether before or after the comparison.

3. The dependent pointer is compared to a pointer that references objects that were last modified a very long time ago, where the only unconditionally safe value of “a very long time ago” is “at compile time”. The key point is that there absolutely must be something other than the address or data dependency that guarantees ordering.

4. Comparisons between two pointers, each of which is carrying a good-enough dependency. For example, you have a pair of pointers, each carrying a dependency, and you want to avoid deadlock by acquiring locks of the pointed-to data elements in address order.

5. The comparison is not-equal, and the compiler does not have enough other information to deduce the value of the pointer carrying the dependency.

Pointer comparisons can be quite tricky, and so it is well worth working through the example shown in Listing 15.28. This example uses a simple struct foo shown on lines 1-5 and two global pointers, gp1 and gp2, shown on lines 6 and 7, respectively. This example uses two threads, namely updater() on lines 9-22 and reader() on lines 24-39.

The updater() thread allocates memory on line 13, and complains bitterly on line 14 if none is available. Lines 15-17 initialize the newly allocated structure, and then line 18 assigns the pointer to gp1. Lines 19 and 20 then update two of the structure’s fields, and does so after line 18 has made those fields visible to readers. Please note that unsynchronized update of reader-visible fields often constitutes a bug. Although there are legitimate use cases doing just this, such use cases require more care than is exercised in this example.

Finally, line 21 assigns the pointer to gp2.

The reader() thread first fetches gp2 on line 30, with lines 31 and 32 checking for NULL and returning if so. Line 33 then fetches field ->b. Now line 34 fetches gp1, and if line 35 sees that the pointers fetched on lines 30 and 34 are equal, line 36 fetches p->c. Note that line 36 uses pointer p fetched on line 30, not pointer q fetched on line 34.

But this difference might not matter. An equals comparison on line 35 might lead the compiler to (incorrectly) conclude that both pointers are equivalent, when in fact they carry different dependencies. This means that the compiler might well transform line 36 to instead be r2 = q->c, which might well cause the value 44 to be loaded instead of the expected value 144.

In short, some care is required in order to ensure that dependency chains in your source code are still dependency chains once the compiler has gotten done with them.

15.3.3 Control-Dependency Calamities

Control dependencies are especially tricky because current compilers do not understand them and can easily break them. The rules and examples in this section are intended to help you prevent your compiler’s ignorance from breaking your code.

A load-load control dependency requires a full read memory barrier, not simply a data dependency barrier. Consider the following bit of code:

1 q = READ_ONCE(x); 
2 if (q) { 
3 	<data dependency barrier> 
4 	q = READ_ONCE(y); 
5 }

This will not have the desired effect because there is no actual data dependency, but rather a control dependency that the CPU may short-circuit by attempting to predict the outcome in advance, so that other CPUs see the load from y as having happened before the load from x. In such a case what’s actually required is:

1 q = READ_ONCE(x); 
2 if (q) { 
3 	<read barrier> 
4 	q = READ_ONCE(y); 
5 }

However, stores are not speculated. This means that ordering is provided for loadstore control dependencies, as in the following example:

1 q = READ_ONCE(x); 
2 if (q) 
3 	WRITE_ONCE(y, 1);

Control dependencies pair normally with other types of ordering operations. That said, please note that neither READ_ONCE() nor WRITE_ONCE() are optional! Without the READ_ONCE(), the compiler might combine the load from x with other loads from x. Without the WRITE_ONCE(), the compiler might combine the store to y with other stores to y. Either can result in highly counterintuitive effects on ordering.

Worse yet, if the compiler is able to prove (say) that the value of variable x is always non-zero, it would be well within its rights to optimize the original example by eliminating the “if” statement as follows:

1 q = READ_ONCE(x); 
2 WRITE_ONCE(y, 1);  /* BUG: CPU can reorder!!! */

It is tempting to try to enforce ordering on identical stores on both branches of the “if” statement as follows:

1 q = READ_ONCE(x); 
2 if (q) { 
3 	barrier(); 
4 	WRITE_ONCE(y, 1); 
5 	do_something(); 
6 } else { 
7 	barrier(); 
8 	WRITE_ONCE(y, 1); 
9 	do_something_else(); 
10 }

Unfortunately, current compilers will transform this as follows at high optimization levels:

1 q = READ_ONCE(x); 
2 barrier(); 
3 WRITE_ONCE(y, 1);  /* BUG: No ordering!!! */
4 if (q) { 
5 	do_something(); 
6 } else { 
7 	do_something_else(); 
8 }

Now there is no conditional between the load from x and the store to y, which means that the CPU is within its rights to reorder them: The conditional is absolutely required, and must be present in the assembly code even after all compiler optimizations have been applied. Therefore, if you need ordering in this example, you need explicit memory-ordering operations, for example, a release store:

1 q = READ_ONCE(x); 
2 if (q) { 
3 	smp_store_release(&y, 1); 
4 	do_something(); 
5 } else { 
6 	smp_store_release(&y, 1); 
7 	do_something_else(); 
8 }

The initial READ_ONCE() is still required to prevent the compiler from proving the value of x.

In addition, you need to be careful what you do with the local variable q, otherwise the compiler might be able to guess the value and again remove the needed conditional. For example:

1 q = READ_ONCE(x); 
2 if (q % MAX) { 
3 	WRITE_ONCE(y, 1); 
4 	do_something(); 
5 } else { 
6 	WRITE_ONCE(y, 2); 
7 	do_something_else(); 
8 }

If MAX is defined to be 1, then the compiler knows that (q%MAX) is equal to zero, in which case the compiler is within its rights to transform the above code into the following:

1 q = READ_ONCE(x); 
2 WRITE_ONCE(y, 2); 
3 do_something_else();

Given this transformation, the CPU is not required to respect the ordering between the load from variable x and the store to variable y. It is tempting to add a barrier() to constrain the compiler, but this does not help. The conditional is gone, and the barrier() won’t bring it back. Therefore, if you are relying on this ordering, you should make sure that MAX is greater than one, perhaps as follows:

1 q = READ_ONCE(x); 
2 BUILD_BUG_ON(MAX <= 1); 
3 if (q % MAX) { 
4 	WRITE_ONCE(y, 1); 
5 	do_something(); 
6 } else { 
7 	WRITE_ONCE(y, 2); 
8 	do_something_else(); 
9 }

Please note once again that the stores to y differ. If they were identical, as noted earlier, the compiler could pull this store outside of the “if” statement.

You must also avoid excessive reliance on boolean short-circuit evaluation. Consider this example:

1 q = READ_ONCE(x); 
2 if (q || 1 > 0) 
3 	WRITE_ONCE(y, 1);

Because the first condition cannot fault and the second condition is always true, the compiler can transform this example as following, defeating control dependency:

1 q = READ_ONCE(x); 
2 WRITE_ONCE(y, 1);

This example underscores the need to ensure that the compiler cannot out-guess your code. More generally, although READ_ONCE() does force the compiler to actually emit code for a given load, it does not force the compiler to use the results.

In addition, control dependencies apply only to the then-clause and else-clause of the if-statement in question. In particular, it does not necessarily apply to code following the if-statement:

1 q = READ_ONCE(x); 
2 if (q) { 
3 	WRITE_ONCE(y, 1); 
4 } else {
5 	WRITE_ONCE(y, 2); 
6 } 
7 WRITE_ONCE(z, 1);  /* BUG: No ordering. */

It is tempting to argue that there in fact is ordering because the compiler cannot reorder volatile accesses and also cannot reorder the writes to y with the condition. Unfortunately for this line of reasoning, the compiler might compile the two writes to y as conditional-move instructions, as in this fanciful pseudo-assembly language:

1 ld r1,x 
2 cmp r1,$0 
3 cmov,ne r4,$1 
4 cmov,eq r4,$2 
5 st r4,y 
6 st $1,z

A weakly ordered CPU would have no dependency of any sort between the load from x and the store to z. The control dependencies would extend only to the pair of cmov instructions and the store depending on them. In short, control dependencies apply only to the stores in the “then” and “else” of the “if” in question (including functions invoked by those two clauses), not to code following that “if”.

Finally, control dependencies do not provide cumulativity. 12 This is demonstrated by two related litmus tests, namely Listings 15.29 and 15.30 with the initial values of x and y both being zero.

The exists clause in the two-thread example of Listing 15.29 (C-LB+o-cgt-o+ocgt-o.litmus) will never trigger. If control dependencies guaranteed cumulativity (which they do not), then adding a thread to the example as in Listing 15.30 (CWWC+o-cgt-o+o-cgt-o+o.litmus) would guarantee the related exists clause never to trigger.

But because control dependencies do not provide cumulativity, the exists clause in the three-thread litmus test can trigger. If you need the three-thread example to provide ordering, you will need smp_mb() between the load and store in P0(), that is, just before or just after the “if” statements. Furthermore, the original two-thread example is very fragile and should be avoided.

The following list of rules summarizes the lessons of this section:

1. Compilers do not understand control dependencies, so it is your job to make sure that the compiler cannot break your code.

2. Control dependencies can order prior loads against later stores. However, they do not guarantee any other sort of ordering: Not prior loads against later loads, nor prior stores against later anything. If you need these other forms of ordering, use smp_rmb(), smp_wmb(), or, in the case of prior stores and later loads, smp_mb().

3. If both legs of the “if” statement begin with identical stores to the same variable, then those stores must be ordered, either by preceding both of them with smp_ mb() or by using smp_store_release() to carry out the stores. Please note that it is not sufficient to use barrier() at beginning of each leg of the “if” statement because, as shown by the example above, optimizing compilers can destroy the control dependency while respecting the letter of the barrier() law.

4. Control dependencies require at least one run-time conditional between the prior load and the subsequent store, and this conditional must involve the prior load. If the compiler is able to optimize the conditional away, it will have also optimized away the ordering. Careful use of READ_ONCE() and WRITE_ONCE() can help to preserve the needed conditional.

5. Control dependencies require that the compiler avoid reordering the dependency into nonexistence. Careful use of READ_ONCE(), atomic_read(), or atomic64_read() can help to preserve your control dependency.

6. Control dependencies apply only to the “then” and “else” of the “if” containing the control dependency, including any functions that these two clauses call. Control dependencies do not apply to code following the end of the “if” statement containing the control dependency.

7. Control dependencies pair normally with other types of memory-ordering operations.

8. Control dependencies do not provide cumulativity. If you need cumulativity, use smp_mb().

In short, many popular languages were designed primarily with single-threaded use in mind. Successfully using these languages to construct multi-threaded software requires that you pay special attention to your memory references and dependencies.

15.4 Hardware Specifics

略。

15.5. WHERE IS MEMORY ORDERING NEEDED?

Memory-ordering operations are only required where there is a possibility of interaction involving at least two variables between at least two threads. As always, if a single-threaded program will provide sufficient performance, why bother with parallelism? 15 After all, avoiding parallelism also avoids the added cost of memory-ordering operations.

If all thread-to-thread communication in a given cycle use store-to-load links (that is, the next thread’s load returning the value that the previous thread stored), minimal ordering suffices, as illustrated by Listings 15.12 and 15.13. Minimal ordering includes dependencies, acquires, and all stronger ordering operations.

If all but one of the links in a given cycle is a store-to-load link, it is sufficient to use release-acquire pairs for each of those store-to-load links, as illustrated by Listings 15.23 and 15.24. You can replace a given acquire with a a dependency in environments permitting this, keeping in mind that the C11 standard’s memory model does not permit this. Note also that a dependency leading to a load must be headed by a lockless_ dereference() or an rcu_dereference(): READ_ONCE() is not sufficient. Never forget to carefully review Sections 15.3.2 and 15.3.3, because a dependency broken by your compiler is no help at all! The two threads sharing the sole non-store-to-load link can usually substitute WRITE_ONCE() plus smp_wmb() for smp_store_release() on the one hand, and READ_ONCE() plus smp_rmb() for smp_load_acquire() on the other.

If a given cycle contains two or more non-store-to-load links (that is, a total of two or more load-to-store and store-to-store links), you will need at least one full barrier between each pair of non-store-to-load links in that cycle, as illustrated by Listing 15.19 as well as in the answer to Quick Quiz 15.23. Full barriers include smp_mb(), successful full-strength non-void atomic RMW operations, and other atomic RMW operations in conjunction with either smp_mb__before_atomic() or smp_mb__after_atomic(). Any of RCU’s grace-period-wait primitives (synchronize_rcu() and friends) also act as full barriers, but at even greater expense than smp_mb(). With strength comes expense, though the overhead of full barriers usually hurts performance more than it hurts scalability.

Note that these are the minimum guarantees. Different architectures may give more substantial guarantees, as discussed in Section 15.4, but they may not be relied upon outside of code specifically designed to run only on the corresponding architecture.

One final word of advice: Again, use of raw memory-ordering primitives is a last resort. It is almost always better to use existing primitives, such as locking or RCU, that take care of memory ordering for you.