CH10-数据结构

访问数据的效率如此重要，因此对算法的讨论也包括相关数据结构的时间复杂度。然而，对于并行程序，时间复杂度的度量还必须包括并发效应。如前所述，这些效应可能是压倒性的因素，这意味着对并发数据结构的设计，必须要像关注串行数据结构中时间复杂度一样关注并发复杂度。

例子

我们将使用薛定谔的动物园这个应用来评估性能。薛定谔拥有一个动物园，里面有大量的动物，他想使用内存数据库来记录他们。动物园中的每个动物在数据库中都有一个条目，每个动物都有一个唯一的名称作为主键，同时还有与每个动物有关的各种数据。

出生、捕获、购买将导致数据插入，而死亡、释放和销售将导致数据删除。因为薛定谔的动物园包括了大量短命动物，包括老鼠可昆虫，所以数据库必须能够支持高频更新请求。

对薛定谔的动物感兴趣的人可以查阅它们，但是，薛定谔已经注意到他的猫拥有非常高的查询率，多到以至于他怀疑是他的老鼠们在使用数据库来查询它们的天敌。这意味着薛定谔的应用必须支持对单个数据条目的高频查询请求。

记住这个应用程序，这里面包含了大量的数据结构。

可分割的数据结构

如今的计算机世界使用了各种各样的数据结构，市面上讲数据结构的教科书多如牛毛。本节专注于单个数据结构，即哈希表。这种方法允许我们更深入地研究如何与并发数据结构交互，同时也能让我们更加熟悉这个在实践中大量应用的数据结构。

哈希表的设计

第六章中强调了通过分割来获得可观性能和扩展性的必要，因此可分割性必须是选择数据结构的首要标准。并行性的主力军——哈希表——很好的满足了这个标准。哈希表在概念上非常简单，包含一个哈希桶的数组。哈希函数将指定数据的键映射到哈希桶元素，也就是存储数据的地方。因此，每个哈希桶有一个数据元素的链表，称为哈希链。如果配置得当，这些哈希链会相当短，允许哈希表可以非常有效地访问任意指定的元素。

另外，每个桶可以有自己的锁，所以哈希表中不同的桶可以完全独立的插入、删除和查找。因此，包含大量元素的哈希表提供了极好的可扩展性。

哈希表的实现

1 struct ht_elem { 
2 	struct cds_list_head hte_next; 
3 	unsigned long hte_hash; 
4 }; 
5 
6 struct ht_bucket { 
7 	struct cds_list_head htb_head; 
8 	spinlock_t htb_lock; 
9 }; 
10 
11 struct hashtab { 
12 	unsigned long ht_nbuckets; 
13 	struct ht_bucket ht_bkt[0]; 
14 };

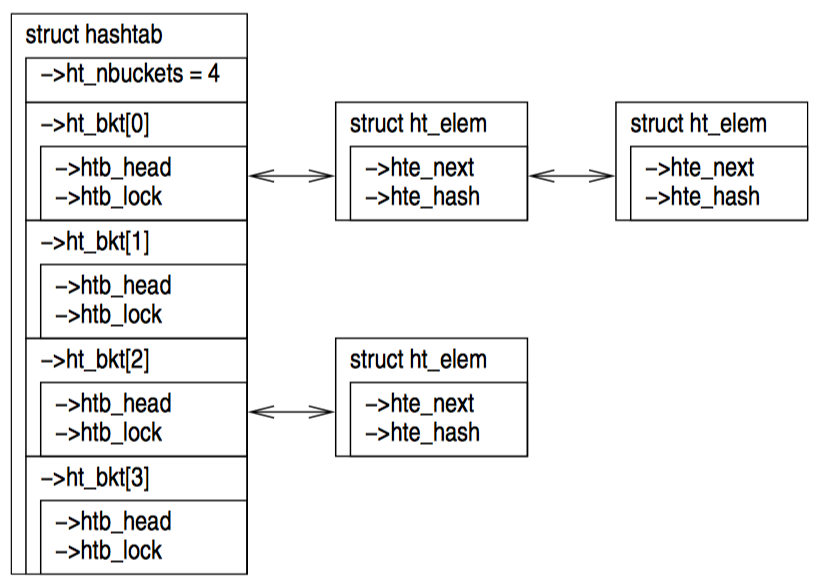
上面的片段展示了简单的固定大小的哈希表使用的一组数据结构，使用链表和每哈希桶的锁。下面的片段展示了如何将它们组合在一起。hashtab 结构包含了 4 个 ht_bucket 结构，->bt_nbuckets 字段代表桶的数量。每个桶都包含链表头 ->htb_head 和锁 ->htb_lock。链表元素 htb_elem 结构通过它们的 ->hte_next 字段找到下一个元素，每个 ht_elem 结构在 ->hte_hash 字段中缓存相应元素的哈希值。ht_elem 结构嵌入在哈希表中的另一个较大结构里，并且这个较大结构可能包含了复杂的键。

下面的片段展示了映射和加解锁函数。第 1~2 行定义了宏 HASH2BKT，它将哈希值映射到相应的 ht_bucket 结构体。这个宏使用了一个简单的模数，如果需要更好的哈希函数，调用者需要自行实现从数据键到哈希值的映射函数。剩下的两个函数分别获取和释放与指定的哈希桶对应的 ->htb_lock 锁。

1 #define HASH2BKT(htp, h) \ 
2 		(&(htp)->ht_bkt[h % (htp)->ht_nbuckets]) 
3 
4 static void hashtab_lock(struct hashtab *htp, 
5 							unsigned long hash) 
6 { 
7 	spin_lock(&HASH2BKT(htp, hash)->htb_lock); 
8 } 
9 
10 static void hashtab_unlock(struct hashtab *htp, 
11 								unsigned long hash) 
12 { 
13 	spin_unlock(&HASH2BKT(htp, hash)->htb_lock); 
14 }

下面的片段展示了 hashtab_lookup，如果指定的键或哈希值存在，它返回一个指向元素的指针，否则返回 NULL。此函数同时接受哈希值和指向键的指针，因为这允许此函数的调用者使用任意的键和哈希函数，cmp 函数指针用于传递比较键的函数，类似于 qsort 的方式。第 11 行将哈希值映射成指向相应哈希桶的指针。第 12~19 行的循环每次执行检查哈希桶中链表的一个元素。第 15 行检查是否与哈希值匹配，如果否，则第 16 行前进到下一个元素。第 17 行检查是否与实际的键匹配，如果是，则第 18 行返回指向匹配元素的指针。如果没有与之匹配的元素，则第 20 行返回 NULL。

1 struct ht_elem * 
2 hashtab_lookup(struct hashtab *htp, 
3 				unsigned long hash, 
4 				void *key, 
5 				int (*cmp)(struct ht_elem *htep, 
6 							void *key)) 
7 { 
8 	struct ht_bucket *htb; 
9 	struct ht_elem *htep; 
10 
11 	htb = HASH2BKT(htp, hash); 
12 	cds_list_for_each_entry(htep, 
13 							&htb->htb_head, 14 hte_next) { 
15 		if (htep->hte_hash != hash) 
16 			continue; 
17 		if (cmp(htep, key)) 
18 			return htep; 
19 	} 
20 	return NULL; 
21 }

下面的片段是 hashtab_add 和 hashtab_del 函数，分别从哈希表中添加和删除元素。

1 void 
2 hashtab_add(struct hashtab *htp, 
3 				unsigned long hash, 
4 				struct ht_elem *htep) 
5 { 
6 	htep->hte_hash = hash; 
7 	cds_list_add(&htep->hte_next, 
8 				&HASH2BKT(htp, hash)->htb_head); 
9 } 
10 
11 void hashtab_del(struct ht_elem *htep) 
12 { 
13 	cds_list_del_init(&htep->hte_next); 
14 }

hashtab_add 函数只是简单的在第 6 行设置元素的哈希值，然后将其添加到第 7~8 行的相应桶中。hashtab_del 函数简单地从哈希桶的链表中移除指定的元素，因为是双向链表所以这很容易。在调用这个函数中任何一个之前，调用者需要确保此时没有其他线程正在访问或修改相同的哈希桶，例如，可以通过事先调用 hashtab_lock 来加以保护。

下面的片段展示了 hashtab_alloc 和 hashtab_free 函数，分别负责表的分配和释放。分配从第 7~9 行开始，分配使用的是系统内存。如果第 10 行检测到内存已耗尽，则第 11 行返回 NULL 给调用者。否则，第 12 行将初始化桶的数量，第 13~16 行的循环初始化桶本身，第 14 行初始化链表头，第 15 行初始化锁。最后，第 17 行返回一个指向新分配哈希表的指针。第 20~23 行的 hashtab_free 函数则直接了当地释放内存。

1 void 
2 hashtab_add(struct hashtab *htp, 
3			 unsigned long hash, 
4 			 struct ht_elem *htep) 
5 { 
6 	htep->hte_hash = hash; 
7 	cds_list_add(&htep->hte_next, 
8 				&HASH2BKT(htp, hash)->htb_head); 
9 } 
10 
11 void hashtab_del(struct ht_elem *htep) 
12 { 
13 	cds_list_del_init(&htep->hte_next); 
14 }

哈希表的性能

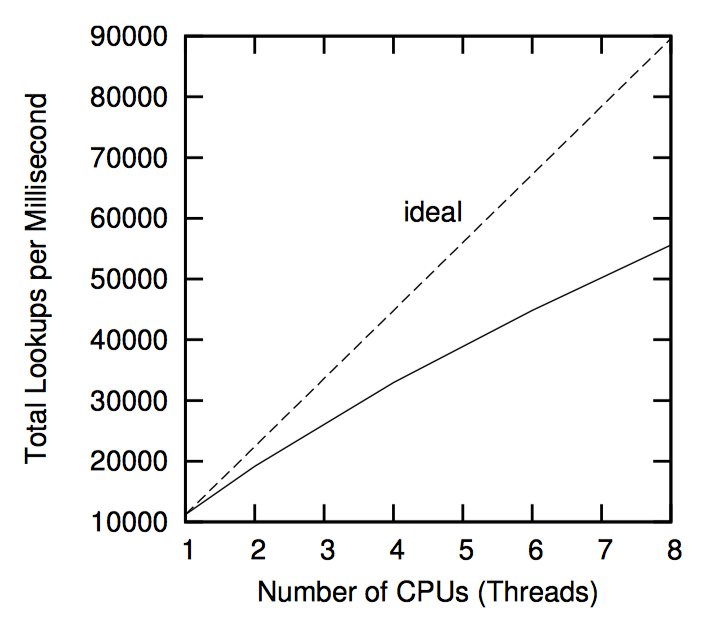
上图展示的是在 8 核 2GHZ Intel Xeon 系统上的性能测试结果，使用的哈希表具有 1024 个桶，每个桶带有一个锁。性能的扩展性几乎接近线性，但是即使只有 8 个 CPU，性能已经不到理想性能水平的一半。产生这个缺口的一部分原因是由于虽然在单 CPU 上获取和释放锁不会产生高速缓存未命中，但是在两个或更多 CPU 上则不然。

随着 CPU 数目的增加，情况只有变得更糟，如下图所示。

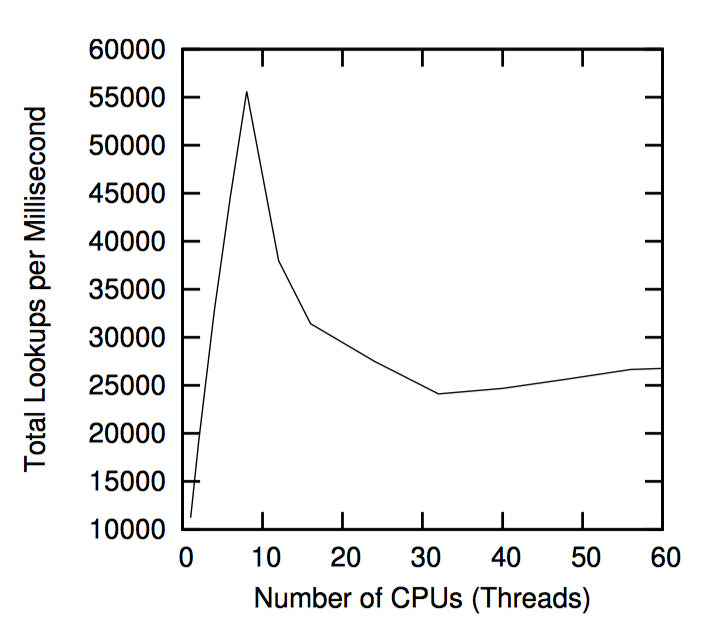
我们甚至不需要额外的线来表示理想性能， 9 个或 9 个以上的 CPU 时性能非常糟糕。这显然警示了我们按照中等数量的 CPU 外推性能的危险。

当然，性能大幅下降的一个原因可能是哈系桶数目的不足。毕竟，我们没有将哈系桶填充到占据一条完整的缓存行，因此每条缓存行有多个哈系桶。这可能是在 9 个 CPU 上导致高速缓存颠簸的原因。当然这一点很容易通过增加哈希桶的数量来验证。

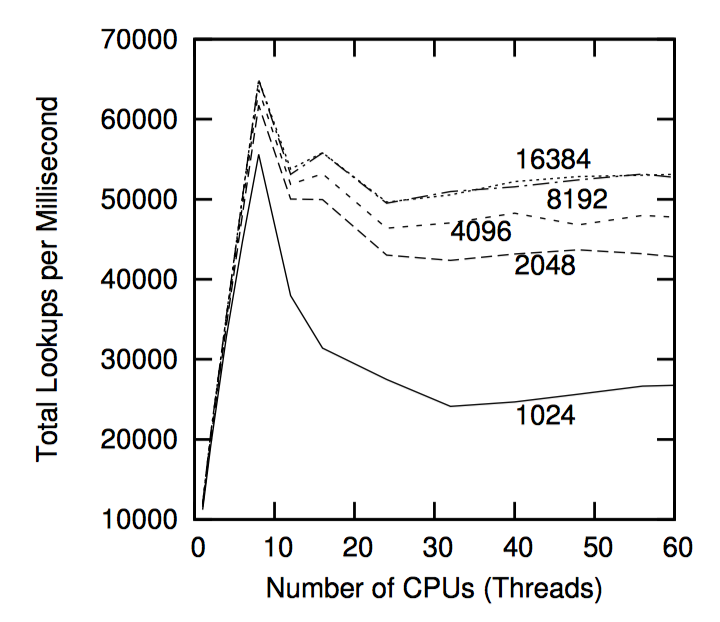
如上图所示，虽然增加了哈系统的数量后性能确实有点提高，可扩展性仍然惨不忍睹。特别是，我们还是看到 9 个 CPU 之后性能会急剧下降。此外，从 8192 个桶增加到 16384 个桶，性能几乎没有提升。显然还有别的东西再捣鬼。

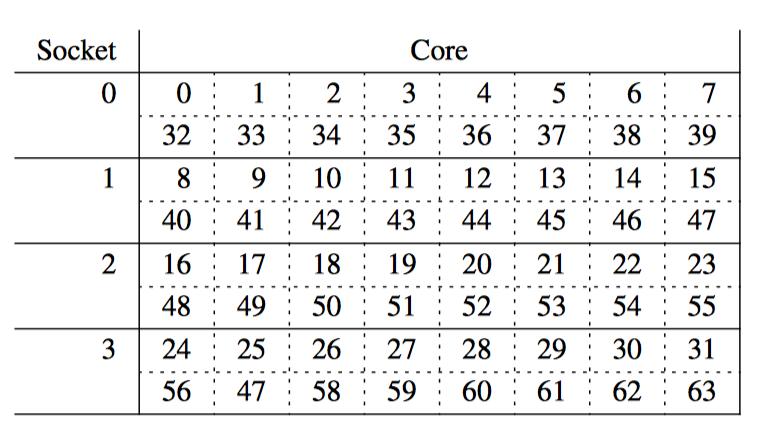
其实这是多 CPU 插槽系统惹的祸，CPU 0~7 和 32~39 会映射到第一个槽位，如下图所示。因此测试程序只用前 8 个 CPU 时性能相当好，但是测试涉及到插槽 0 的 CPU 0~7 和插槽 1 的 CPU 8 时，会产生跨插槽边界数据传递的开销。如果前所述，这可能会验证降低性能。总之，对于多插槽系统来说，除了数据结构完全分割之外，还需要良好的局部性访问能力。

读侧重的数据结构

虽然通过分割数据结构可以帮助我们带来出色的可扩展性，但是 NUMA 效应也会导致性能和扩展性的严重恶化。另外，要求读者互斥写者也可能会导致在读侧重的场景下的性能。然而，我们可以通过使用前面介绍的 RCU 来实现性能和可扩展性的双丰收。使用危险指针也可以达到类似的效果。

受 RCU 保护的哈希表实现

对于受 RCU 保护的每桶一锁的哈希表，写者按照上节描述的方式使用锁，但读者使用 RCU。数据结构、HASH2BKT、hashtab_lock、hashtab_unlock 函数与上一节保持一致。但是读者使用拥有更轻量级并发控制的 hashtab_lock_lookup。如下片段所示：

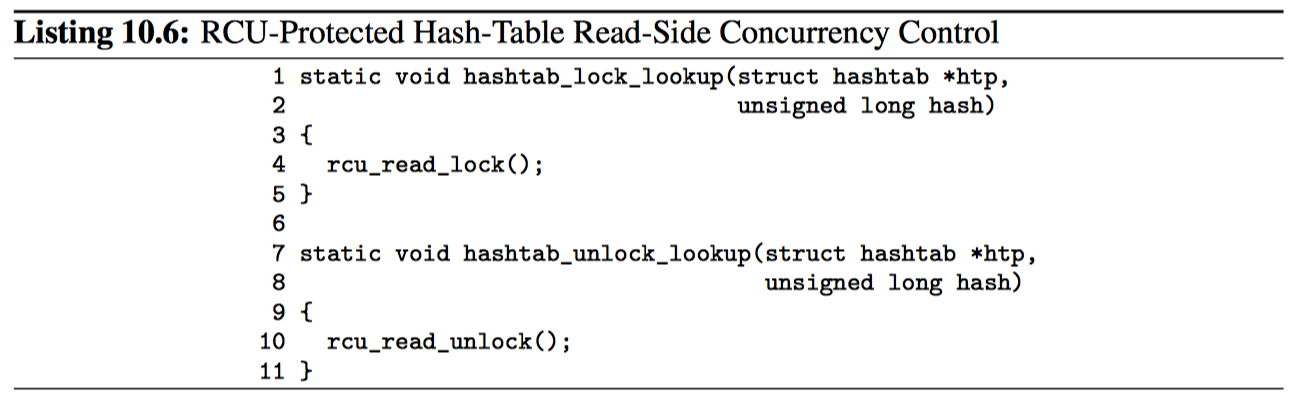
下面的片段则展示了 hashtab_lookup 函数的实现。这与前面的实现类似，除了将 cds_list_for_each_entry 替换为 cds_list_for_each_entry_rcu。这两个原语都按照顺序遍历 htb->htb_head 指向的哈希链表，但是 cds_list_for_each_entry_rcu 还要强制执行内存屏障以应对并发插入的情况。这是两种哈希表实现的重大区别，与纯粹的每桶一锁实现不同，受 RCU 保护的实现允许查找、插入、删除操作同时运行，支持 RCU 的 cds_list_for_each_entry_rcu 可以正确处理这种增加的并发性。还要主要 hashtab_lookup 的调用者必须在 RCU 读端临界区内，例如，调用者必须在调用 hashtab_lookup 之前调用 hashtab_lock_lookup(当前在之后还要调用 hashtab_unlock_lookup)。

下面的片段展示了 hashtab_add 和 hashtab_del，两者都是非常类似于其在非 RCU 哈希表实现中的对应函数。hashtab_add 函数使用 cds_list_add_rcu 而不是 cds_list_add，以便在有人正在查询哈希表时，将元素安装正确的排序添加到哈希表。hashtab_del 函数使用 cds_list_del_rcu 而不是 cds_list_del_init，它允许在查找到某数据元素后该元素马上被删除的情况。和 cds_list_del_init 不同，cds_list_del_rcu 仍然保留该元素的前向指针，这样 hashtab_lookup 可以遍历新删除元素的后继元素。

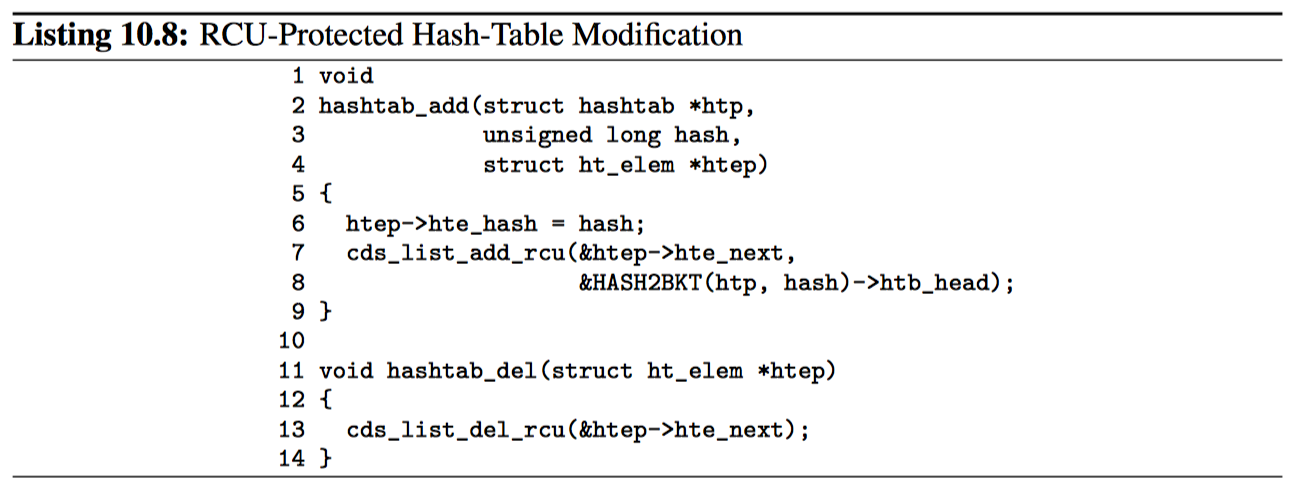
当让，在调用 hashtab_del 之后，调用者必须等待一个 RCU 宽限期(例如在释放或以其他方式重用新删除元素的内存之前调用 syncronize_rcu)。

受 RCU 保护的哈希表的性能

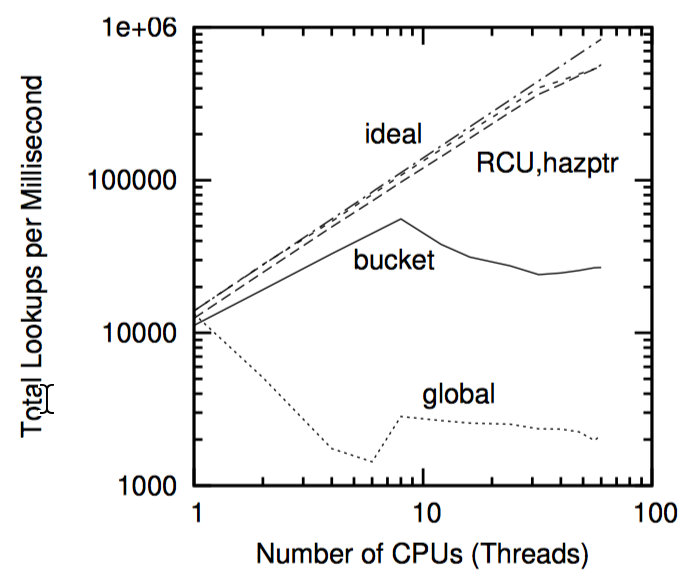
上图展示了受 RCU 保护的和受危险指针保护的只读哈希表的性能，同时与上一节的每桶一锁实现做比较。如你所见，尽管 CPU 数和 NUMA 效应更大，RCU 和危险指针实现都能接近理想的性能和可扩展性。使用全局锁的实现的性能也在图中给出了标示，正如预期一样，其结果针织比每桶一锁的实现更加糟糕。RCU 做得比危险指针稍微好一些，但在这个以对数刻度表示的图中很难看出差异来。

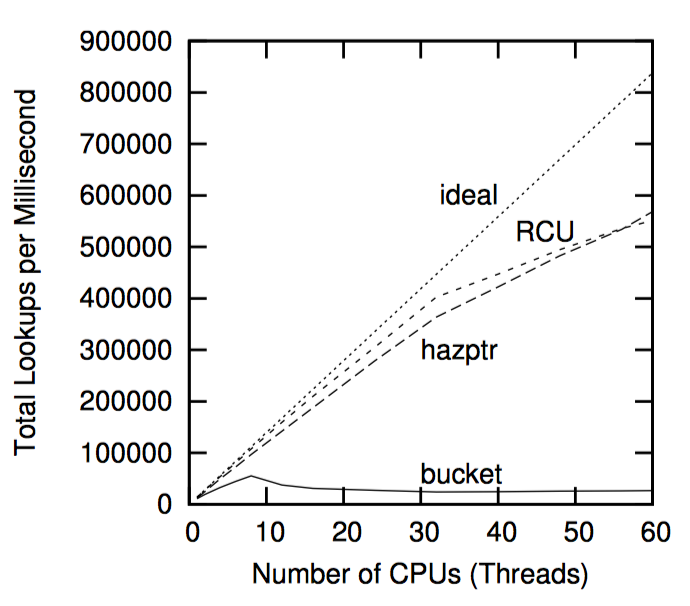
上图显示了线性刻度上的相同数据。这使得全局锁实现基本和 X 轴平行，但也更容易辨别 RCU 和危险指针的相对性能。两者都显示在 32 CPU 处的斜率变化，这是由于硬件多线程的缘故。当使用 32 个或更少的 CPU 时，每个线程都有自己的 CPU 时，每个线程都有自己的 CPU 核。在这种情况下，RCU 比危险指针做的更好，因为危险指针的读取端内存屏障会导致 CPU 时间的浪费。总之，RCU 比危险指针能更好地利用每个硬件线程上的 CPU 核。

如前所述，薛定谔对他的猫的受欢迎程度感到惊讶，但是随后他认识到需要在他的设计中考虑这种受欢迎程度。下图显示了程序在 60 个 CPU 上运行的结果，应用程序除了查询猫咪以外什么也不做。对这个挑战，RCU 和危险指针实现的表现很好，但是每桶一锁实现的负载为负，最终性能比全局锁实现还差。我们不应该对此感到吃惊，因为如果所有的 CPU 都在查询猫咪，对应于猫的那个桶的锁实际上就是全局锁。

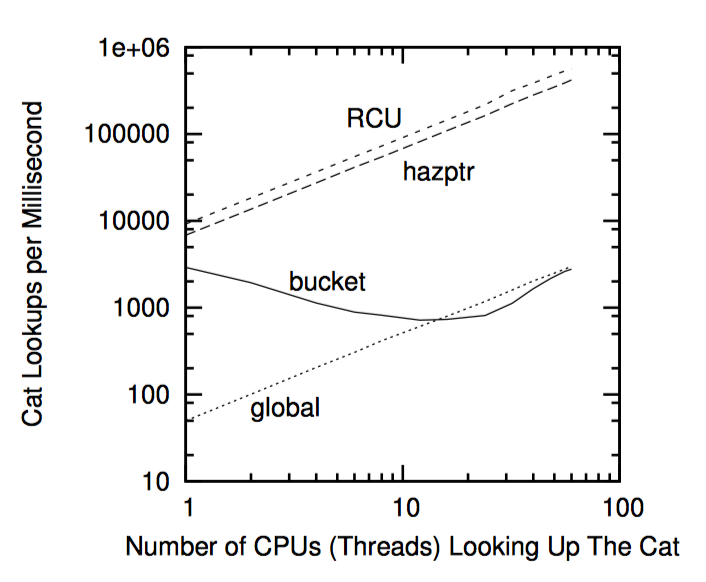
这个只有猫的基准测试显示了数据分片方法的一个潜在问题。只有与猫的分区关联的 CPU 才能访问有关猫的数据，这限制了只查询猫时系统的吞吞量。当然，有很多应用程序可以将数据均匀地分散，对于这些应用，数据分片非常适用。然而，数据分片不能很好地处理“热点”，由薛定谔的猫触发的热点只是其中一个例子。

当然，如果我们只是去读数据，那么一开始我们并不需要任何并发控制。因此，下图显示修正后的结果。在该图的最左侧，所有 60 个 CPU 都在进行查找，在图的最右侧，所有 60 个 CPU 都在做更新。对于哈希表的 4 种实现来说，每毫秒查找数随着做更新的 CPU 数量的增加而减少，当所有 60 个 CPU 都在更新时，每毫秒查找数达到 0。相对于危险指针 RCU 做的更好一些，因为危险指针的读取端内存屏障在有更新存在时产生了更大的开销。这似乎也说明，现代硬件大大优化了内存屏障的执行，从而大幅减少了在只读情况下的内存屏障开销。

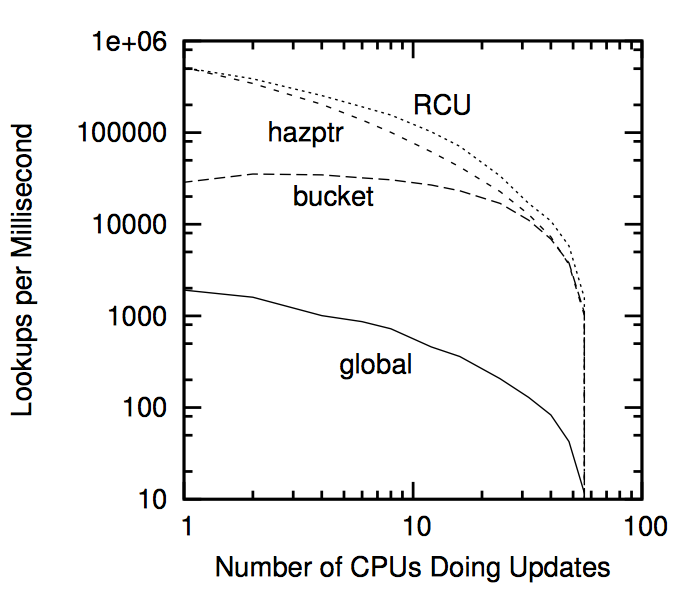
上图展示了更新频率增加对查找的影响，而下图则显示了更新频率的增加对更新本身的影响。危险指针和 RCU 从一开始就占据领先，因为，与每桶一锁不同，危险指针和 RCU 的读者并不排斥写者。然而，随着做更新操作的 CPU 数量的增加，开始显示出更新端开销的存在，首先是 RCU，然后是危险指针。当然，所有这三种实现都要比全局锁实现更好。

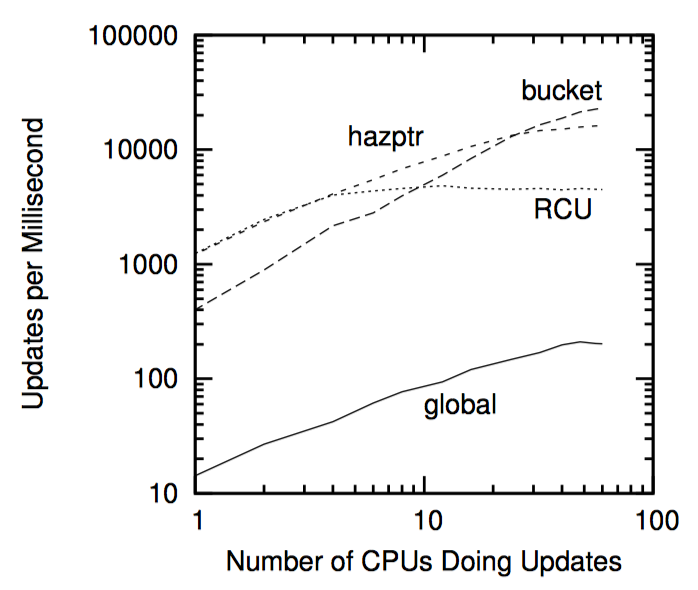
当然，很可能查找性能的差异也受到更新速率差异的影响。为了检查这一点，一种方法是人为地限制每桶一锁和危险指针实现的更新速率，以匹配 RCU 的更新速率。这样做显然不会显著提高每桶一锁实现的查找性能，也不会拉近危险指针与 RCU 之间的差距。但是，去掉危险指针的读取端内存屏障(从而导致危险指针的实现不安全)确实弥合了危险指针和 RCU 之间的差距。虽然这种不安全的危险指针实现通常足够可靠，足以用于基准测试用途，但是绝对不推荐用于生产用途。

对受 RCU 保护的哈希表的讨论

RCU 实现和危险指针会导致一种后果，一对并发读者可能会不同意猫此时的状态。比如，其中在某只猫被删除之前，一个读者可能已经提取了指向猫的数据结构的指针，而另一个读者可能在之后获得了相同的指针。第一个读者会相信那只猫还活着，而第二个读者会相信猫已经死了。

当然，薛定谔的猫不就是这么一回事吗，但事实证明这对于正常的非量子猫也是相当合理的。

合理的原因是，我们我发准确得知动物出生或死亡的时间。

为了搞明白这一点，让我们假设我们可以通过心跳检查来测得猫的死亡。这又带来一个问题，我们应该在最后一次心跳之后等待多久才宣布死亡。只等待 1ms？这无疑是荒谬的，因为这样一只健康活猫也会被宣布死亡——然后复活，而且每秒钟还发生不止一次。等待一整个月也是可笑的，因为到那时我们通过嗅觉手段也能非常清楚地知道，这只可怜的猫已经死亡。

因为动物的心脏可以停止几秒钟，然后再次跳动，因此及时发现死亡和假警概率之间存在一种权衡。在最后一次心跳和死亡宣言之间要等待多久，两个兽医很有可能不同意彼此的意见。例如，一个兽医可能声明死亡发生在最后一次心跳后 30s，而另一个可能要坚持等待完整的一分钟。在猫咪最后一次心跳后第二个 30s 周期内，两个兽医会对猫的状态有不同的看法。

当然，海森堡教导我们生活充满了这种不确定性，这也是一件好事，因为计算机硬件和软件的行为在某种程度上类似。例如，你怎么知道计算机有个硬件出问题了呢？通常是因为它没有及时回应。就像猫的心跳，折让硬件是否有故障出现了一个不确定性窗口。

此外，大多数的计算机系统旨在与外部世界交互。因此，对外的一致性是至关重要的。然而，正如我们在前面看到的，增加内部的一致性常常以外部一致性作为代价。像 RCU 和危险指针这样的技术放弃了某种程度上的内部一致性，以获得改善后的外部一致性。

总之，内部一致性不一定是所有问题域关心的部分，而且经常在性能、可扩展性、外部一致性或者所有上述方面产生巨大的开销。

不可分割的数据结构

固定大小的哈希表可以完美分割，但是当可扩展的哈希表在增长或收缩时，就不那么容易分割了。不过事实证明，对于受 RCU 保护的哈希表，完全可以写出高性能并且可扩展的实现。

可扩展哈希表的设计

与 21 世纪初的情况形成鲜明对比的是，现在有不少于三个不同类型的可扩展的受 RCU 保护的哈希表实现。第一个也是最简单的一个是 Herbert Xu 为 Linux 内核开发的实现，我们首先来介绍它。

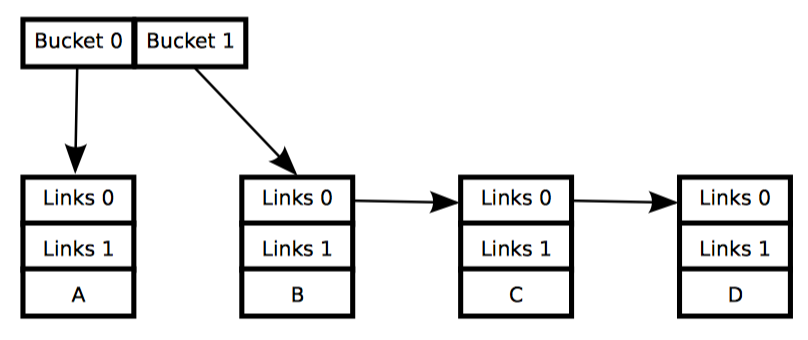
这个哈希表实现背后的关键之处，是每个数据元素可以有两组链表指针，RCU 读者(以及非 RCU 的写者)使用其中一组，而另一组则用于构造新的可扩展的哈希表。此方法允许在哈希表调整大小时，可以并发地执行查找、插入和删除操作。

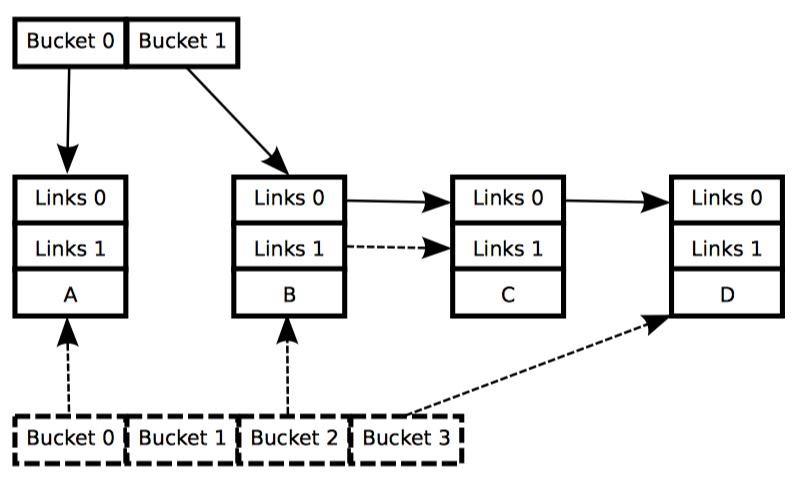
调整大小操作的过程下图 1~4 所示，图 1 展示了两个哈希桶的初始状态，时间从图 2 推进到 图 3。初始状态使用 0 号链表来将元素与哈希桶链接起来。然后分配一个包含 4 个桶的数组，并且用 1 号链表将进入 4 个新的哈希桶的元素链接起来。者产生了如图 2 所示的状态(b)，此时 RCU 读者仍让使用原来的两桶数组。

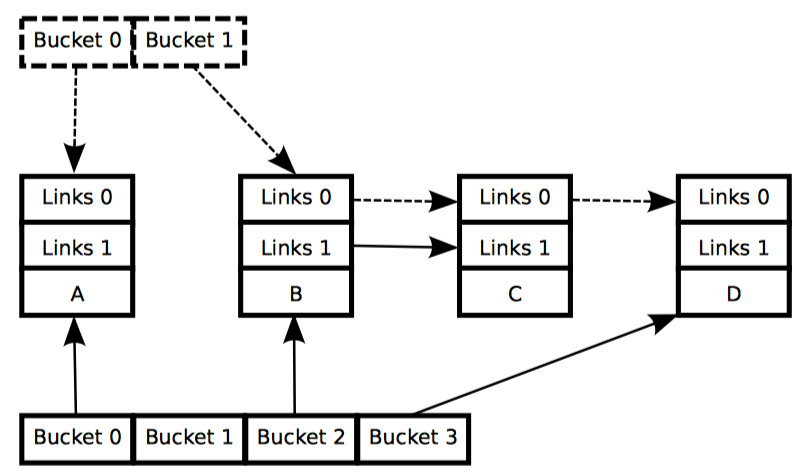
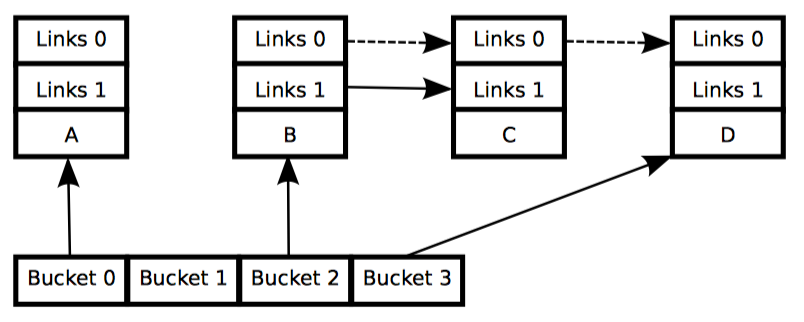
随着新的四桶数组暴露给读者，紧接着是等待所有老读者完成读取的宽限期操作，产生如图 3 所示的状态(c)。这时，所有 RCU 读者都开始使用新的四桶数组，这意味着现在可以释放旧的两桶数组，产生图 4 所示的状态(d)。

可扩展哈希表的实现

调整大小操作是通过插入一个中间层次的经典方法完成的，这个中间层次如下面的片段中 12~25 行的结构体 ht 所示。第 27~30 行所示的是结构体 hashtab 仅包含指向当前 ht 结构的指针以及用于控制并发地请求调整哈希大小的自旋锁。如果我们使用传统的基于锁或原子操作的实现，这个 hashtab 结构可能会称为性能和可扩展性的严重瓶颈。但是，因为调整大小操作应该相对少见，所以这里 RCU 应该能帮我们大忙。

结构体 ht 表示哈希表的尺寸信息，其大小第 13 行的 ->ht_nbuckets 字段指定。为了避免出现不匹配的情况，哈希表的大小和哈系统的数组(第 24 行 ->ht_btk[])存储于相同的结构中。第 14 行上的 ->ht_resize_cur 字段通常等于 -1，当正在进行调整大小操作时，该字段的值表示其对应数据已经添入新哈希表的哈希桶索引，如果当前没有进行调整大小的操作，则 ->ht_new 为 NULL。因此，进行调整大小操作本质上就是通过分配新的 ht 结构体并让 ->ht_new 指针指向它，然后没遍历一个旧表的桶就前进一次 ->ht_resize_cur。当所有元素都移入新表时，hashtab 结构的 ->ht_cur 字段开始指向新表。一旦所有的旧 RCU 读者完成读取，就可以释放旧哈希表的 ht 结构了。

第 16 行的 ->ht_idx 字段指示哈希表实例此时应该使用哪一组链表指针，ht_elem 结构体里的 ->hte_next[] 数组用该字段作为此时的数组下标，见第 3 行。

第 17~23 行定义了 ->ht_hash_private、->ht_cmp、->ht_gethash、->ht_getkey 等字段，分别代表着每个元素的键和哈希函数。->ht_hash_private 用于扰乱哈希函数，其目的是防止通过对哈希函数所使用的参数进行统计分析来发起拒绝服务攻击。->ht_cmp 函数用于比较两个键，->ht_gethash 计算指定键的哈希值，->ht_getkey 从数据中提取键。

ht_bucket 结构与之前相同，而 ht_elem 结构与先前实现的不同仅在于用两组链表指针代替了代替了先前的单个链表指针。

在固定大小的哈希表中，对桶的选择非常简单，将哈希值转换成相应的桶索引。相比之下，当哈希表调整大小时，还有必要确定此时应该从旧表还是新表的哈希桶中进行选择。如果旧表中要选择的桶已经被移入新表中，那么应该从新表中选择存储桶。相反，如果旧表中要选择的桶还没有被移入新表，则应从旧表中选择。

桶的选择如相面的代码所示，包括第 1~8 行的 ht_get_bucket_single 和第 10~24 行的 ht_get_bucket。ht_get_bucket_single 函数返回一个指向包含指定键的桶，调用时不允许发生调整大小的操作。第 5~6 行，他还将与键相对应的哈希值存储到参数 b 指向的内存。第 7 行返回对应的桶。

ht_get_bucket 函数处理哈希表的选择，在第 16 行调用 ht_get_bucket_single 选择当前哈希表的哈希值对应的桶，用参数 b 存储哈希值。如果第 17 行确定哈希表正在调整大小，并且第 16 行的桶已经被移入新表，则第 18 行选择新的哈希表，并且第 19 行选择新表中的哈希值对应的桶，并再次用参数 b 存储哈希值。

如果第 21 行确定参数 i 为空，则第 22 行记录当前使用的是哪一组链表指针。最后，第 23 行返回指向所选哈希桶的指针。

这个实现的 ht_get_bucket_single 和 ht_get_bucket 允许查找、修改和调整大小操作同时执行。

读取端的并发控制由 RCU 提供。但是更新端的并发控制函数 hashtab_lock_mod 和 hashtab_unlock_mod 现在需要处理并发调整带下操作的可能性，如下片段所示：

第 1~19 行是 hashtab_lock_mod，第 9 行进入 RCU 读端临界区，以放置数据结构在遍历期间被释放，第 10 行获取对当前哈希表的引用，然后第 11 行获得哈希桶所对应的键的指针。第 12 行获得了哈希桶的锁，这将防止任何并发的调整大小操作移动这个桶，当然如果调整大小操作已经移动了该桶，则这一步没有任何效果。然后第 13 行检查并发的调整大小操作是否已经将这个桶移入新表。然后第 13 行检查并发的调整大小操作是否已经将这个桶移入新表，如果没有，则第 14 行在持有所选桶的锁时返回(此时仍处于 RCU 读端临界区内)。

否则，并发的调整大小操作将此桶移入新表，因此第 15 行获取新的哈希表，第 16 行选择键对应的桶。最后，第 17 行获取桶的锁，第 18 行释放旧表的桶的锁。最后，hashtab_lock_mod 退出 RCU 读端临界区。

hashtab_unlock_mod 函数负责释放由 hashtab_lock_mod 获取的锁。第 28 行能拿到当前哈希表，然后第 29 行调用 ht_get_bucket，以获得键锁对应的桶的指针，当让该桶可能已经位于新表。第 30 行释放桶的锁，以及最后第 31 行退出 RCU 读端临界区。

现在已经有了桶选择和并发控制逻辑，我们已经准备好开始搜索和更新哈希表了。如下所示的 hashtab_lookup、hashtab_add、hashtab_del 函数：

上面第 1~21 行的 hashtab_lookup 函数执行哈希查找。第 11 行获取当前哈希表，第 12 行获取指定键对应的桶的指针。当调整大小操作已经越过该桶在旧表中的位置时，则该桶位于新表中。注意，第 12 行业传入了表明使用哪一组链表指针的索引。第 13~19 行的循环搜索指定的桶，如果第 16 行检测到匹配的桶，第 18 行则返回指向包含数据元素的指针。否则如果没有找到匹配的桶，第 20 行返回 NULL 表示失败。

第 23~37 行的 hashtab_add 函数向哈希表添加了新的数据元素。第 32~34 行获取指定键对应的桶的指针(同时提供链表指针组下标)。第 35 行如前所述，为哈希表添加新元素。在这里条用者需要处理并发性，例如在调用 hashtab_add 前后分别调用 hashtab_lock_mod 和 hashtab_unlock_mod。这两个并发控制函数能正确地与并发调整大小操作互相同步：如果调整大小操作已经超越了该数据元素被添加到的桶，那么元素将添加到新表中。

第 39~52 行的 hashtab_del 函数从哈希表中删除一个已经存在的元素。与之前一样，第 48~50 行获取桶并传入索引，第 51 行删除指定元素。与 hashtab_add 一样，调用者负责并发控制，并且需要确保并发控制可以处理并发调整大小的操作。

实际调整大小由 hashtab_resize 执行，如上所示。第 17 行有条件地获取最顶层的 ht_lock，如果获取失败，则第 18 行返回 EBUSY 以表明正在进行调整大小操作。否则，第 19 行获取当前哈希表的指针，第 21~24 行分配所需大小的新哈希表。如果指定了新的哈希函数，将其应用于表，否则继续使用旧哈希表的哈希函数。如果第 25 行检测到内存分配失败，则第 26 行释放 htlock 锁并且在第 27 行返回出错的原因。

第 29 行开始桶的移动过程，将新表的指针放入酒标的 ht_new 字段，第 30 行确保所有不知道新表存在的读者在调整大小操作继续之前完成释放。第 31 行获取当前表的链表指针索引，并将其存储到新表中，以防止两个哈希表重写彼此的链表。

第 33~44 行的循环每次将旧表的一个桶移动到新的哈希表中。第 34 行将获取旧表的当前桶的指针，第 35 行获取该桶的自旋锁，并且第 36 行更新 ht_resize_cur 以表明此桶正在移动中。

第 37~42 行的循环每次从旧表的桶中移动一个元素到对应新表的桶中，在整个操作期间持有新表桶中的锁。最后，第 43 行释放旧表中的桶锁。

一旦执行到 45 行，所有旧表的桶都已经被移动到新表。第 45 行将新创建的表视为当前表，第 46 行等待所有的旧读者(可能还在引用旧表)完成。然后第 47 行释放调整大小操作的锁，第 48 行释放旧的哈希表，最后第 49 行返回成功。

可扩展哈希表的讨论

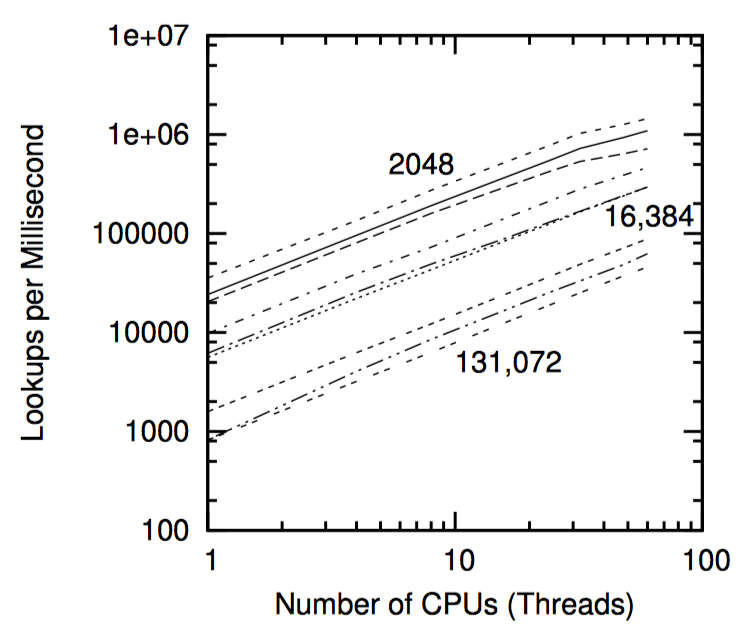
上图比较了可扩展哈希表和固定哈希表在拥有不同元素数量下的性能。图中为每种元素个数绘制了三条曲线。

最上面的三条线是有 2048 个元素的哈希表，这三条线分别是：2048 个桶的固定哈希表、1024 个桶的固定哈希表、可扩展哈希表。这种情况下，因为哈希链很短因此正常的查找开销很低，因此调整大小的开销反而占据主导地位。不过，因为桶的个数越多，固定大小哈希表性能优势越大，至少在给予足够操作暂停时间的情况下，调整大小操作还是有用的，一次 1ms 的暂停时间显然太短。

中间三条线是 16348 个元素的哈希表。这三条线分别是：2048 个桶的固定哈希表、可扩展哈希表、1024 个桶的固定哈希表。这种情况下，较长的哈希链将导致较高的查找开销，因此查找开销大大超过了调整哈希表大小的操作开销。但是，所有这三种方法的性能在 131072 个元素时比在 2048 个元素时差一个数量级以上，这表明每次将哈希表大小增加 64 倍才是最佳策略。

该图的一个关键点是，对受 RCU 保护的可扩展哈希表来说，无论是执行效率还是可扩展性都是与其固定大小的对应者相当。当然在实际调整大小过程中的性能还是受到一定程度的影响，这是由于更新每个元素的指针时产生了高速缓存未命中，当桶的链表很短时这种效果最显著。这表明每次调整哈希表的大小时应该一步到位，并且应该防止由于频繁的调整操作而导致的性能下降，在内存宽裕的环境中，哈希表大小的增长幅度应该比缩小时的幅度更大。

该图的另一个关键点是，虽然 hashtab 结构体是不可分割的，但是它特使读侧重的数据结构，这说明可以使用 RCU。鉴于无论是在性能还是在扩展性上，可扩展哈希表都非常接近于受 RCU 保护的固定大小哈希表，我们必须承认这种方法是相当成功的。

最后，请注意插入、删除和查找操作可以与调整大小操作同时进行。当调整元素个数极多的哈希表大小时，需要重视这种并发性，特别是对于那些必须有严格响应是时间限制的应用程序来说。

当然，ht_elem 结构的两个指针集合确实会带来一定的内存开销，我们将在下一节展开讨论。

其他可扩展哈希表

上一节讨论的可扩展哈希表，其缺点之一就是消耗的内存大。每个数据元素拥有两对链表指针。是否可以设计一种受 RCU 保护的可扩展哈希表，但链表只有一对？

答案是“是”。Josh Triplett 等人创造了一种相对(relativistic)哈希表，可以递增地分割和组合相应的哈希链，以便读者在调整大小操作期间始终可以看到有效的哈希链。这种增量分割和组合取决于一点事实，读者可以看到在其他哈希链中的数据元素。这一点是无害的，当发生这种情况时，读者可以简单地忽略这些由于键不匹配而看见的无关数据元素。

上图展示了如何将相对哈希表缩小两倍的过程。此时，两个桶的哈希表收缩成一个桶的哈希表，又称为线性链表。这个过程将较大的旧表中的桶合并为较小的新标中的桶。为了让这个过程正常进行，我们显然需要限制两个表的哈希函数。一种约束是在底层两个表中使用相同的哈希函数，但是当从大到小收缩时去除哈希值的最低位。例如，旧的两桶哈希表使用哈希值的高两位，而新的单桶哈希表使用哈希值的最高位。这样，在较大的旧表中相邻的偶数和奇数桶可以合并成较小的新表中的单个桶里，同时哈希值仍然可以覆盖单桶中的所有元素。

初始状态显示在图的顶部，从初始状态(a)开始，时间从顶部到底部前进，收缩过程从分配新的较小数组开始，并且使新数组的每个桶都指向旧表中相应桶的第一个元素，到达状态(b)。

然后，两个哈希链连接在一起，到达状态(c)。在这种状态下，读了偶数编号元素的读者看不出有什么变化，查找元素 1 和 3 的读者同样也看不到变化。然而，查找其他奇数编号元素的读者会遍历元素 0 和 2。这样做是无害的，因为任何奇数键都不等于这两个元素。这里会有一些性能损失，但是另一方面，这与新表完全就位以后将经历的性能损失完全一样。

接下来，读者可以开始访问新表，产生状态(d)。请注意，较旧的读者可能仍然在遍历大哈希表，所以在这种状态下两个哈希表都在使用。

下一步是等待所有旧的读者完成，产生状态(e)。

在这种状态下，所有读者都使用新表，以便旧表中桶可以被释放，最终到达状态(f)。

扩展相对哈希表的过程与收缩相反，但需要更多的宽限期步骤，如下图。

在该图的顶部是初始状态(a)，时间从顶部前进到底部。

一开始我们分配较大的哈希表，带有两个桶，到达状态(b)。请注意，这些新桶指向旧桶对应部分的第一个元素。当这些新桶被发布给读者后，到达状态(c)。过了宽限期后，所有读者都将使用新的大哈希表，到达状态(d)。在这个状态下，只有那些遍历偶数值哈希桶的读者才会遍历到元素 0，因此现在的元素 0 是白色的。

此时，旧表的哈希桶可以被释放，但是在很多实现中仍然使用这些旧桶来跟踪将链表元素“解压缩”到对应新桶中的进度。在对这些元素的第一遍执行中，最后一个偶数编号的元素其“next”指针将指向后面的偶数编号元素。在随后的宽限期操作之后，到达状态(e)。垂直箭头表示要解压缩的下一个元素，元素 1 的颜色现在为黑色，表示只有那些遍历奇数哈希桶的读者才可以接触到它。

接下来，在对这些元素的第一遍执行中，最后一个奇数编号的元素其“next”指针将指向后面的奇数编号元素。在随后的宽限期操作之后，到达状态(f)。最后的解压缩操作(包括宽限期操作)到达最终状态(g)。

简而言之，相对哈希表减少了每个元素的链表指针的数量，但是在调整大小期间产生额外的宽限期。一般来说这些额外的宽限期不是问题，因为插入、删除和查找可能与调整大小同时进行。

结果证明，完全可以将每元素的内存开销从一对指针降到一个指针，同时保留 O(1) 复杂度的删除操作。这是通过使用受 RCU 保护的增广拆序链表(split-order list)做到的。哈希表中的数据元素被排列成排序后的单向链表，每个哈希桶指向该桶中的第一个元素。通过设置元素的 next 指针的低阶位来标记为删除，并且在随后的遍历中再次访问这些元素时将它们从链表中移除。

受 RCU 保护的拆序链表非常复杂，但是为所有插入、删除、查找操作提供无锁的进度保证。在实时应用中这种保证及其重要。最新版本的用户态 RCU 库提供了一个实现。

其他数据结构

前面的小节主要关注因为可分割性而带来的高并发性数据结构，高效的处理读侧重的访问模式，或者应用读侧重性来避免不可分割性。本节会简要介绍其他数据结构。

哈希表在并行应用上的最大优点之一就是它是可以完全分割的，至少是在不调整大小时。一种保持可分割性的尺寸独立性的方法是使用基树(radix tree)。也称 trie。Trie 将需要搜索的键进行分割，通过各个连续的键分区来遍历下一级 trie。因此，trie 可以被认为是一组嵌套的哈希表，从而提供所需的可分割性。Trie 的一个缺点是稀疏的键空间导致无法充分利用内存。有许多压缩技术可以解决这个缺点，包括在遍历前将键映射到较小的键空间中。基树在实践中被大量使用，包括在 Linux 内核中。

哈希表和 trie 的一种重要特例，同时也可能是最古老的数据结构，是数组及其多维对应物——矩阵。因为矩阵的可完全分割性质，在并发数值计算算法中大量应用了矩阵。

自平衡树在串行代码中被大量使用，AVL 树和红黑树可能是最著名的例子。早期尝试并行化 AVL 树的实现很复杂，效率也很可疑。但是最近关于红黑树的研究是使用 RCU 读者来保护读，哈希后的锁数组来保护写，这种实现提供了更好的性能和可扩展性。事实证明，红黑树的积极再平衡虽然适用于串行程序，但不一定适用于并行场景。因此，最近有文章创造出受 RCU 保护的较少再平衡的“盆景树”，通过付出最佳树深度的代价以获得跟有效的并发更新。

并发跳跃链表(skip list)非常适合 RCU 读者，事实上这代表着早期在学术上对类似 RCU 技术的使用。

前面讨论过的并行双端队列，虽然同是在性能和扩展性上不太令人印象深刻，并行堆栈和并行队列也有着悠久的历史。但是它们往往是并行库具有的共同特征。研究人员最近提出放松堆栈和队列对排序的约束，有一些工作表名放松排序的队列实际上比严格 FIFO 的队列具有更好的排序属性。

乐观来说，未来对并行数据结构的持续研究似乎会产生具有惊人性能的新颖算法。

微优化

以上展示的数据结构都比较直白，没有利用底层系统的缓存层次结构。此外，对于键到哈希值的转换和其他一些频繁的操作，很多实现使用了指向函数的指针。虽然这种方式提供了简单性和可移植性，但在很多情况下会损失一些性能。

以下部分涉及实例化(specializtion)、节省内存、基于硬件角度的考虑。请不要错误的将这些小节看成是本书讨论的主题。市面上已经有大部头讲述如何在特定 CPU 上做优化，更不用说如今常用的 CPU 了。

实例化

前面提到的可扩展哈希表使用不透明类型的键。这给我们带来了极大地灵活性，允许使用任何类型的键，但是由于使用了函数指针，也导致了显著的开销。现在，现代化的硬件使用复杂的分支预测技术来最小化这种开销，但在另一方面，真实世界的软件往往比今天的大型硬件分支越策表可容纳的范围更大。对于调用指针来说尤其如此，在这种情况下，分支预测硬件必须是在分支信息之外另外记录指针信息。

这种开销可以通过实例化哈希表实现来确定键的类型和哈希函数。这样做出列图 10.24 和图 10.25 的 ht 结构体中的 ht_cmp、ht_gethash、ht_getkey 函数指针，也消除了这些指针的相应调用。这使得编译器可以内联生成固定函数，这消除的不仅是调用指令的开销，而且消除了参数打包的开销。

此外，可扩展哈希表的设计考虑了将桶选择与并发控制分离的 API。虽然这样可以用单个极限测试来执行本章中的所有哈希表实现，但是这也意味着许多操作必须将计算哈希值和与可能的大小调整操作交互这些事情来回做两次。在要求性能的环境中，hashtab_lock_mod 函数也可以返回对所选桶的指针，从而避免后续调用 ht_get_bucket。

除此之外，和我在 20 世纪 70 年代带一次开始学习编程相比，现代硬件的一大好处是不太需要实例化。这可比回到 4K 地址空间的时代效率高多了。

比特与字节

本章讨论的哈希表几乎没有尝试节省内存。例如在 10.24 中，ht 结构体的 ht_idx 字段的取值只能是 0 或 1，但是却占用完整的 32 位内存。完全可以删除它，例如，从 ht_resize_key 字段窃取一个比特。因为 ht_resize_key 字段足够大寻址任何内存地址，而且 ht_bucket 结构体总是要比一个字节长，所以 ht_resize_key 字段肯定有多个空闲比特。

这种比特打包技巧经常用在高度复制的数据结构中，就像 Linux 内核中的 page 结构体一样。但是，可扩展哈希表的 ht 结构复制程度并不太高。相反我们应该关注 ht_bucket 结构体。有两个地方可以减小 ht_bucket 结构：将 htb_lock 字段放在 htb_head 指针的低位比特中；减少所需的指针数量。

第一点可以利用 Linux 内核中的位自旋锁，由 include/linux/bit_spinlock.h 头文件提供。他们用在 Linux 内核的内存敏感数据结构中，但也不是没有缺点：

1. 比传统的自旋锁语义慢。
2. 不能参与 Linux 内核中的 lockdep 死锁检测工具。
3. 不记录锁的所有权，想要进一步调试会变得复杂。
4. 不参与 -rt 内核中的优先级提升，这意味着保持位自旋锁时必须禁用抢占，这可能会降级实时延迟。

尽管有这些缺点，位自旋锁在内存十分珍贵时非常有用。

10.4.4 节讨论了第二点的一个方面，可扩展哈希表只需要一组桶链表指针来代替 10.4 节实现中所需的两组指针。另一个办法是使用单链表来替代在此使用的双向链表。这种方式的一个缺点是，删除需要额外的开销：要么标记传出指针以便以后删除、要么通过搜索要删除的元素的桶链表。

简而言之，人们需要在最小内存开销和性能、简单性之间权衡。幸运的是，在现代系统上连接内存允许我们优先考虑性能和简单性，而不是内存开销。然而，即使拥有今天的大内存系统，有时仍然需要采取极端措施以减少内存开销。

硬件层面的考虑

现代计算机通常在 CPU 和主存储器之间移动固定大小的数据块，从 32 字节到 256 字节不等。这些块名为缓存行(cacheline)，如 3.2 节所述，这对于高性能和可扩展性是非常重要的。将不兼容的变量放入同一缓存行会严重降低性能和扩展性。例如，假设一个可扩展哈希表的数据元素具有一个 ht_elem 结构，它与某个频繁增加的计数器处于相同的高速缓存行中。频繁增加的计数器将导致高速缓存行出现在执行增量的 CPU 中。如果其他 CPU 尝试遍历包含数据元素的哈希桶链表，则会导致昂贵的告诉缓存未命中，降低性能和扩展性。

如上图所示，这是一种在 64 位字节高速缓存行的系统上解决问题的方法。这里的 gcc aligned 属性用于强制将 counter 字段和 ht_elem 结构体分成独立的缓存行。这将允许 CPU 全速遍历哈希桶链表，尽管此时计数器也在频繁增加。

当然，这引出了一个问题，“我们怎么知道缓存行是 64 位大小？”。在 Linux 系统中，此信息可以从 /sys/devices/system/cpu/cpu */cache/ 目录得到，甚至有时可以在安装过程重新编译应用程序以适应系统的硬件结构。然而，如果你想要体验困难，也可以让应用程序在非 Linux 系统上运行。此外，即使你满足于运行只有在 Linux 上，这种自修改安装又带来了验证的挑战。

幸运的是，有一些经验法则在实践中工作的相当好，这是作者从一份 1995 年的文件中收到的。第一组规则设计重新排列结构以适应告诉缓存的拓扑结构。

1. 将经常更新的数据与以读为主的数据分开。例如，将读侧重高的数据放在结构的开头，而将频繁更新的数据放于末尾。如果可能，将很少访问的数据放在中间。
2. 如果结构有几组字段，并且每组字段都会在独立的代码路径中被更新，将这些组彼此分开。再次，尽量在不同的组之间放置很少访问的数据。在某些情况下，将每个这样的组放置在被原始结构单独引用的数据结构中也是可行的。
3. 在可能的情况下，将经常更新的数据与 CPU、线程或任务相关联。
4. 在有可能的情况下，应该尽量将数据分割在每 CPU、每线程、每任务。

最近已经有一些朝向基于痕迹的自动重排的结构域的研究。这项工作可能会让优化的工作变得不那么痛苦，从而从多线程软件中获得出色性能和可扩展性。

以下是一组处理锁的额外的经验法则：

1. 当使用高竞争度的锁来保护被频繁更新的数据时，采取以下方式之一：

• 将锁与其保护的数据处于不同的缓存行中。
• 使用适用于高度竞争的锁，例如排队锁。
• 重新设计以减少竞争。

2. 将低度竞争的锁置于与它们保护的数据相同的高速缓存行中。这种方法意味着因锁导致的当前 CPU 的高速缓存未命中同时也带来了它的数据。
3. 使用 RCU 保护读侧重的数据，或者，如果 RCU 不能使用并且临界区非常长时，使用读写锁。

当然这些只是经验法则，而非绝对规则。最好是先做一些实验以找到最适合你的特殊情况的方法。

总结

本章主要关注哈希表，包括不可完全分割的可扩展哈希表。本章关于哈希表的阐述是围绕高性能可扩展数据访问的许多问题的绝佳展示，包括：

1. 可完全分割的数据结构在小型系统上工作良好，比如单 CPU 插槽系统。
2. 对于较大型的系统，需要将局部数据访问性和完全分割同等看待。
3. 读侧重技术，如危险指针和 RCU，在以读为主的工作负载时提供了良好的局部访问性，因此即使在大型系统中也能提供出色的新能和可扩展性。
4. 读侧重技术在某些不可分割的数据结构上也工作得不错，例如可扩展的哈希表。
5. 在特定工作负载时实例化数据可以获得额外的性能和可扩展性，例如，将通用的键替换成 32 位整数。
6. 尽管可移植性和极端性能的要求通常是互相干扰的，但是还是有一些数据结构布局技术可以在这两套要求之间达到良好的平衡。

但是如果没有可靠性，性能和可扩展性也算不上什么。因此下一章将介绍“验证”。