CH06-分割同步设计
本章将描述如何设计能够更好利用多核优势的软件。编写并行软件时最重要的考虑是如何进行分割。正确的分割问题能够让解决方案简单、扩展性好且高性能,而不恰当的分割问题则会产生缓慢且复杂的解决方案。“设计”这个词非常重要:对你来说,应该是分割问题第一、编码第二。顺序颠倒会让你产生极大的挫败感,同时导致软件低劣的性能和扩展性。
分割练习
哲学家就餐
该问题指的是,桌子周围坐着 5 位哲学家,而桌子上每两个哲学家之间有一根叉子,因此是 5 个哲学家 5 根叉子。每个哲学家只能用他左手和右手旁的叉子用餐,一旦开始用餐则不吃到心满意足是不会停下的。
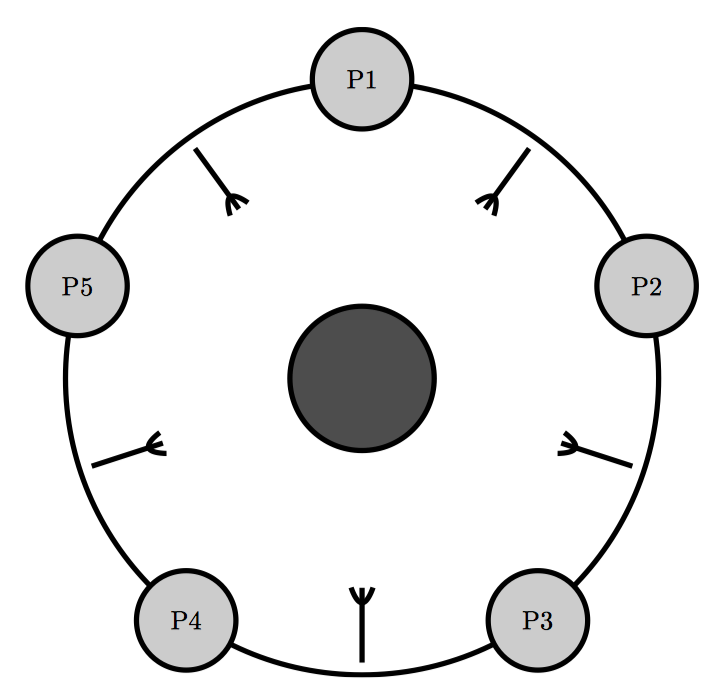
我们的目标就是构建一种算法来阻止饥饿。一种饥饿的场景是所有哲学家都去拿左手边的叉子。因为他们在吃饱前不会放下叉子,并且他们还需要第二把叉子才能开始用餐,所以所有哲学家都会挨饿。注意,让至少一位哲学家就餐并不是我们的目标,即使让个别哲学家挨饿也是要避免的。
Dijkstra 的解决方法是使用一个全局信号量。假设通信延迟忽略不计,这种方法十分完美。因此,近来的解决办法是像下图一样为叉子编号。每个哲学家都先拿他盘子周围编号最小的叉子,然后再拿编号最高的叉子。这样坐在图中最上方的哲学家会先拿起他左手边的叉子,然后是右手边的叉子,而其他哲学家则先拿起右手边的叉子。因为有两个哲学家试着会去拿叉子 1,而只有一位会成功,所以只有 4 位哲学家抢 5 把叉子。至少 4 位中的一位肯定能够拿到两把叉子,这样就能开始就餐了。
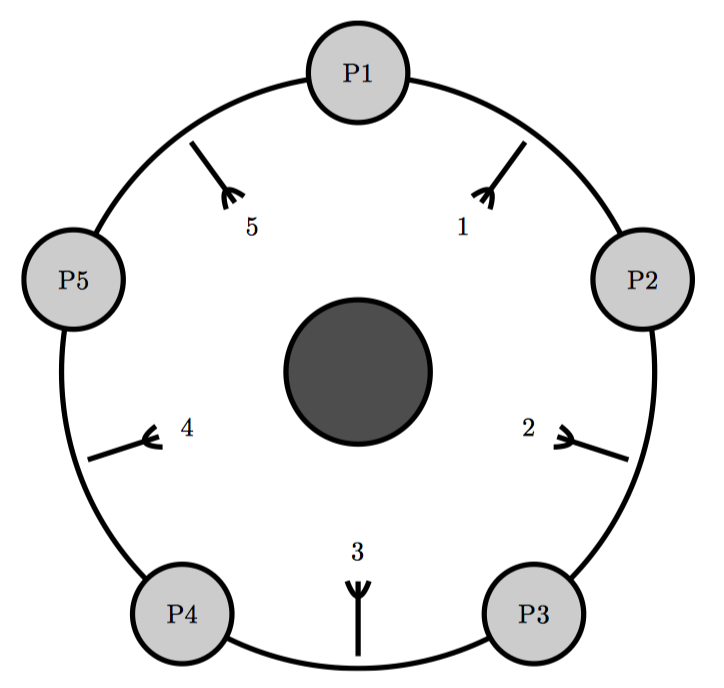
这种为资源编号并按照编号顺序获取资源的通用技术经常在被用在防止死锁上。 但是很容易就能想象出来一个事件序列来产生这种效果:虽然大家都在挨饿,但是一次只有一个哲学家就餐。
- P2 拿起叉子 1,阻止 P1 拿起叉子 1。
- P3 拿起叉子 2。
- P4 拿起叉子 3。
- P5 拿起叉子 4。
- P5 拿起叉子 5,开始就餐。
- P5 放下叉子 4 和 5。
- P4 拿起叉子 4,开始就餐。
简单来说,该算法会导致每次仅有一个哲学家能够就餐,即使 5 个哲学家都在挨饿,但事实上此时有足够的叉子供两名哲学家同时就餐。
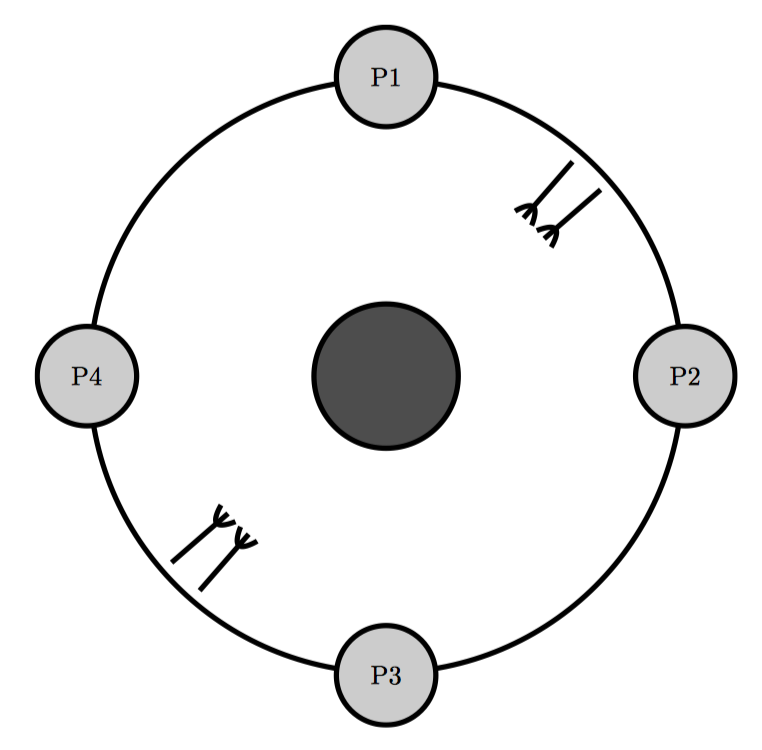
上图是另一种解决方式,里面只有 4 位哲学家,而不是 5 位,这样可以更好的说明分割技术。最上方和最右边的哲学家合用一个叉子,而最下面和最左面的哲学家合用一个叉子。如果所有哲学家同时感觉饿了,至少有两位能够同时就餐。另外如图所示,现在叉子可以捆绑成一对,这样同时拿起或放下,就简化了获取和释放锁的算法。
这是水平化分割的一个例子,或者叫数据并行化,这么叫是因为哲学家之间没有依赖关系。在数处理型的系统中,“数据并行化”是指一种类型的数据只会被多个同类型软件组件中的一个处理。
双端队列
双端队列是一种元素可以从两端插入和删除的数据结构。这里将展示一种分割设计策略,能实现合理且简单的解决方案。
右手锁与左手锁
右手锁与左手锁是一种看起来很直接的办法,为左手端的入列操作添加一个左手锁,为右手端的出列操作添加一个右手锁。但是这种办法的问题是当队列中的元素不足 4 个时,两个锁的返回会发生重叠。这种重叠是由于移动任何一个元素不仅只影响元素本身,还要影响它左边和右边相邻的元素。这种范围在图中被涂上了淹死,蓝色表示左手锁的范围,红色表示右手锁的范围,紫色表示重叠的范围。虽然创建这样一种算法是可能的,但是至少要小心着五种特殊情况,尤其是在队列另一端的并发活动会让队列随时可能从一种特殊情况转变为另外一种特殊情况的场景。所以最好考虑其他解决方案。
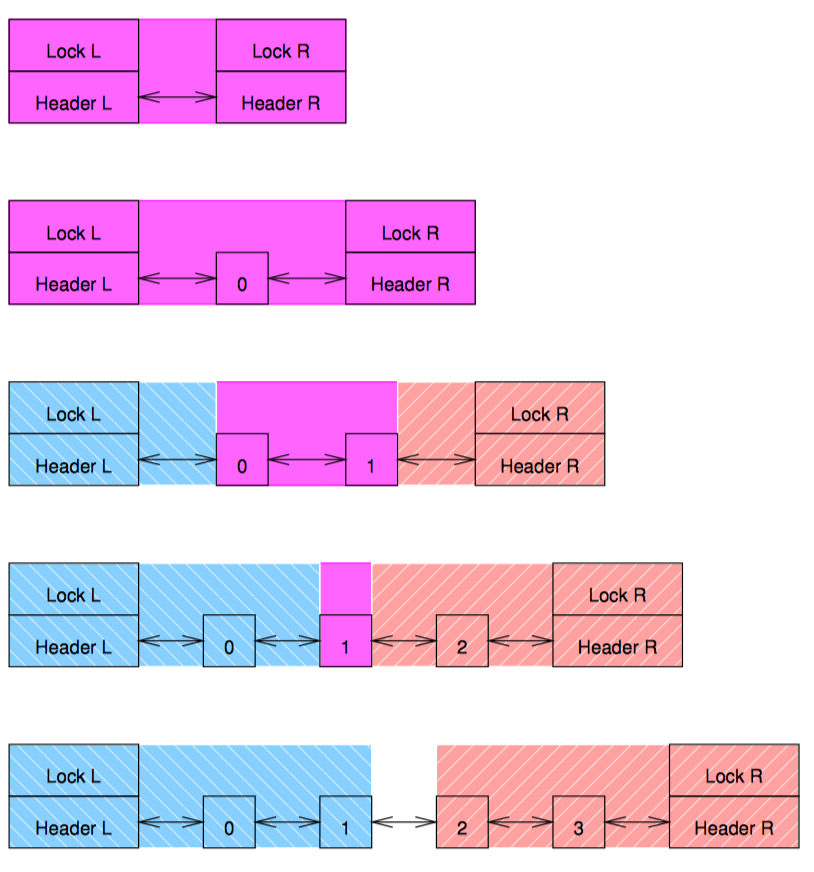
复合双端队列
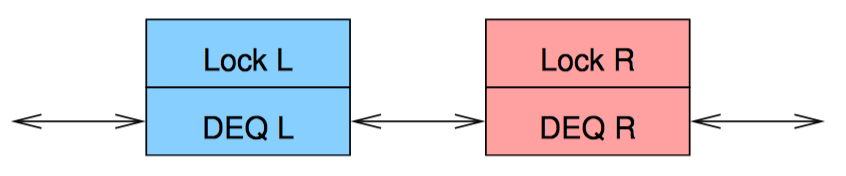
上图是一种强制确保锁的范围不会发生冲突的方法。两个单独的双端队列串联在一起,每个队列用自己的锁保护。这意味着数据偶尔会从双端队列的一列跑到另一列。此时必须同时持有两把锁。为避免死锁,可以使用一种简单的锁层级关系,比如,在获取右手锁前先获取左手锁。这比在同一列上同时使用两把锁要简单的多,因为我们可以无条件的让左边的入列元素进入左手队列,右边的入列元素进入右手队列。主要的复杂度来源于从空队列中出列,这种情况下必须做到如下几点:
- 如果持有右手锁,释放并获取左手锁,重新检查队列释放仍然为空。
- 获取右手锁。
- 重新平衡跨越两个队列的元素。
- 移除指定的元素。
- 释放两把锁。
代码实现也并不复杂,再平衡操作可能会将某个元素在两个队列之间来回移动,这不仅浪费时间,而且想要获得最佳性能,还需针对工作负荷不断微调。
哈希双端队列
哈希永远是分割一个数据结构的最简单有效的方法。可以根据元素在队列中的位置为每个元素分配一个序号,然后以此对双端队列进行哈希,这样第一个从左边进入空队列的元素编号为 0,第一个从右边进入空队列的元素编号为 1。其他从左边进入只有一个元素的队列的元素编号依次递减(-1,-2,-3…),而其他从右边进入只有一个元素的队列的元素编号依次递增(2,3,4…)。关键是,实际上并不用真正为元素编号,元素的序号暗含它们在队列中的位置中。
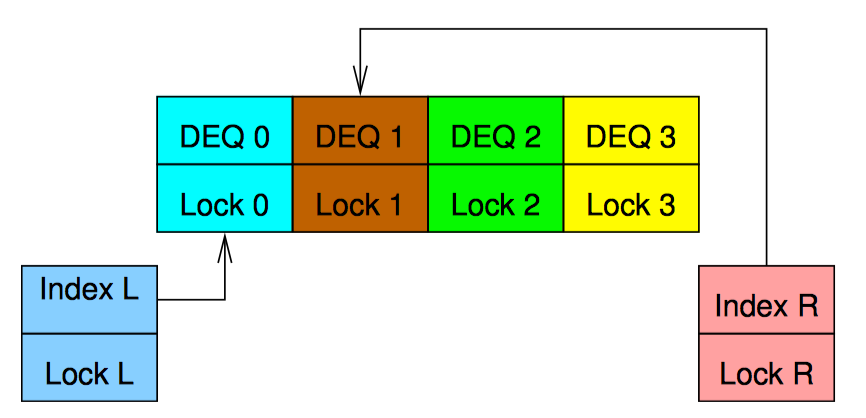
然后,我们用一个锁保护左手下标,用另外一个锁保护右手下标,再各用一个锁保护对应的哈希链表。上图展示了 4 个哈希链表的数据结构。注意锁的范围没有重叠,为了避免死锁,只在获取链表锁之前获取下标锁,每种类型的锁(下标或链表),一次获取从不超过一个。
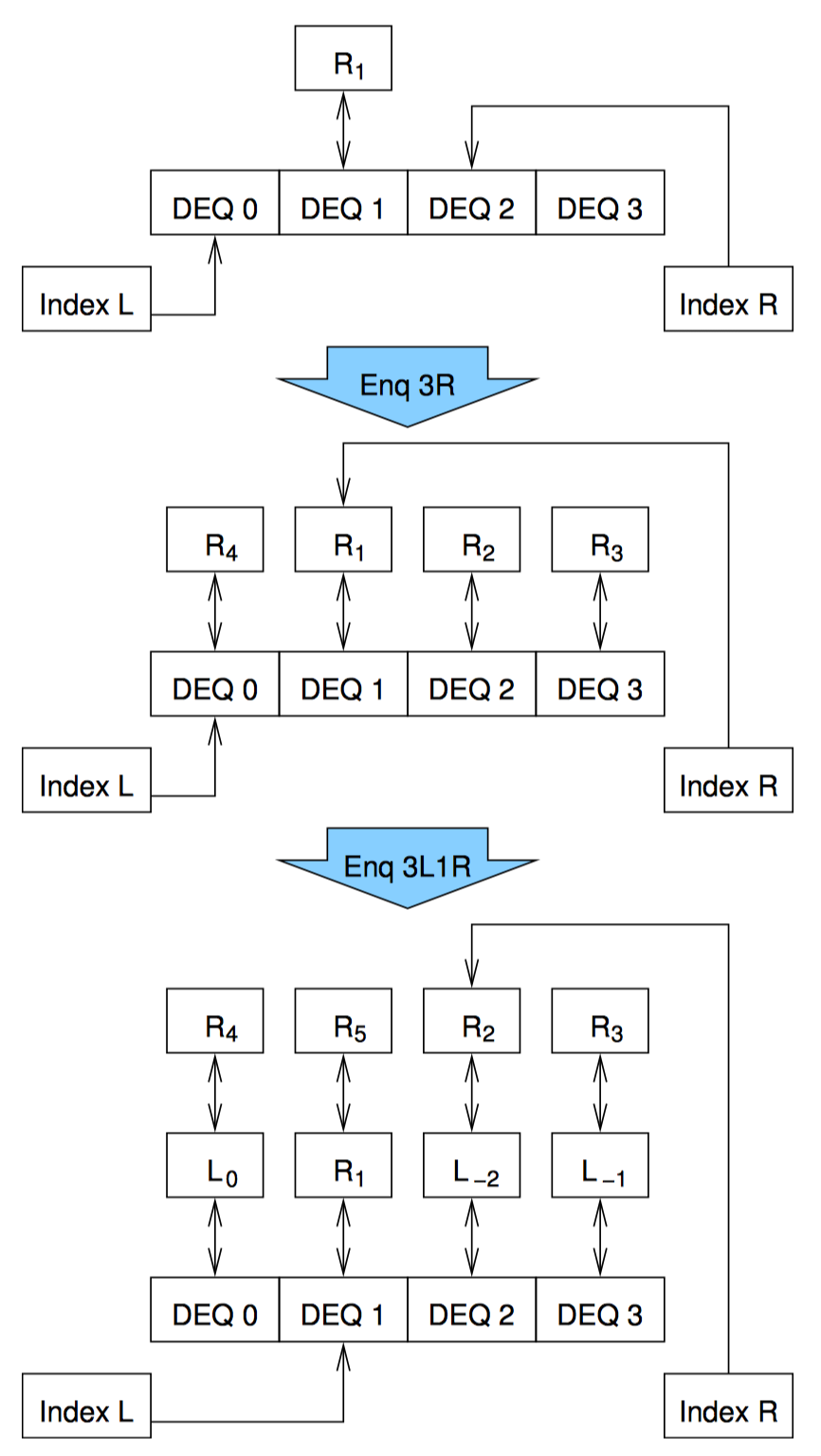
每个哈希链表都是一个双端队列,在这个例子中,每个链表拥有四分之一的队列元素。上图最上面部分是 R1 元素从右边入队后的状态,右手的下标增加,用来引用哈希链表 2。上图第二部分是又有 3 个元素从右手入队。正如你所见,下标回到了它们初始的状态,但是每个哈希队列现在都是非空的。上图第三部分是另外三个元素从左边入队,而另外一个元素从右边入队后的状态。
从上图第三部分的状态可以看出,左出队操作将会返回元素 L-2,并让左手下边指向哈希链 2,此时该链表只剩下 R2。这种状态下,并发的左入队和右入队操作可能会导致锁竞争,但这种锁竞争发生的可能性可以通过使用更大的哈希表来降低。
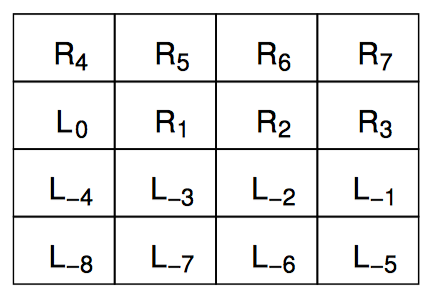
上图展示了 12 个元素如何组成一个有 4 个并行哈希桶的双端队列。每个持有单锁的双端队列拥有整个并行双端队列的四分之一。
双端队列讨论
复合式实现在某种程度上要比哈希式实现复杂,但是仍然属于比较简单的。当然,更加智能的再平衡机制可以非常复杂,但是和软件实现相比,这里使用的软件再平衡机制已经很不错了,这个方法甚至不比使用硬件辅助算法的实现差多少。不过,从这种机制中我们最好也只能获得 2 倍的扩展能力,因为最多只有两个线程并发的持有出列的锁。这个局限同样适用于使用非足额同步方法的算法,比如 Michael 的使用 CAS 的出队算法。
事实上,正如 Dice 等人所说,非同步的单线程双端队列实现性能非常好,比任何他们研究过的并行实现都搞很多。因此,不管哪种实现,由于队列的严格先入先出特性,关键点都在于共享队列中出队或出队的巨大开销。
更近一步,对于严格先入先出的队列,只有在线性化点不对调用者可见时,队列才是严格先入先出。事实上,在事前的例子中“线性化点”都隐藏在带锁的临界区内。而这些队列在单独的指令开始时,并不保证先入先出。这表明对于并发程序来说,严格先入先出的特性并没有那么有价值。实际上 Kirsch 等人已经证明不提供先入先出保证的队列在性能和扩展性上更好。这些例子说明,如果你打算让并发数据出入一个单队列时,真的该重新考虑一下整体设计。
分割讨论
哲学家就餐问题的最后解法是该问题的最优解法,是“水平并行化”或“数据并行化”的极佳例子。在这个例子中,同步的开销接近于 0 或等于 0。相反,双端队列的实现是“垂直并行化”或者“管道”极佳示例,因为数据从一个线程转移到另一个线程。“管道”需要密切合作,因此为获得某种程度上的效率,需要做的工作更多。
设计准则
想要获取最佳的性能和扩展性,简单的办法就是不断尝试,直到你的程序和最优实现水平相当。但是如果你的代码不是短短数行,如何能在浩如烟海的代码中找到最优实现呢?另外,什么才是最优实现呢?前面给出了三个并行编程的目标:性能、生产率和通用性,最优的性能常常要付出生产率和通用性的代价。如果不在设计时就将这些选择考虑进去,就很难在限定的时间内开发出性能良好的并行程序。
但是除此之外,还需要更详细的设计准则来指导实际的设计,这就是本节的主题。在真实的世界中,这些准则将在某种程度上冲突,这需要设计者小心权衡得失。这些准则可以被认为是设计中的阻力,对这些阻力进行恰当权衡,就被称为“设计模式”。
基于三个并行编程目标的设计准则是加速、竞争、开销、读写比率和复杂性。
加速倍速:之所以花费如此多时间和精力进行并行化,加速性能是主要原因。加速倍速的定义是运行程序的顺序执行版本所需要的时间,除以执行并行版本所需时间的比例。
竞争:如果对一个并行程序来说,增加更多的 CPU 并不能让程序忙起来,那么多出来的 CPU 是因为竞争的关系而无法工作。可能是锁竞争、内存竞争或者其他什么性能杀手的原因。
工作-同步比率:单处理器、单线程、不可抢占、不可中断版本的并行程序完全不需要任何同步原语。因此,任何消耗在这些原语上(通信中的高速缓存为命中、消息延迟、加解锁原语、原子指令和内存屏障)的时间都是对程序意图完成的工作没有直接帮助的开销。同步开销与临界区中代码的开销之间的关系是重要的衡量准则,更大的临界区能容忍更大的同步开销。工作-同步开销比率与同步效率的概念有关。
读-写比率:对于极少更新的数据结构,更多是采用“复制”而不是“分割”,并且用非对称的同步原语来保护,以提高写者同步开销的代价来降低读者的同步开销。对频繁更新的数据结构的优化也是可以的。
复杂性:并行程序比相同的顺序执行的程序复杂,这是因为并行程序要比顺序执行程序维护更多的状态,虽然这些状态在某些情况下理解起来很容易。并行程序员必须要考虑同步原语、消息传递、锁的设计、临界区识别以及死锁等诸多问题。
更大的复杂性通常转换为了更高的开发代价和维护代价。因此,对现有程序修改的范围和类型非常受代码预算的限制,因为对原有程序的新年能加速需要消耗相当的时间和精力。在更糟糕的情况,增加复杂性甚至会降低性能和扩展性。
进一步说,在某种范围内,还可以对顺序执行程序进行一定程度的优化,这笔并行化更廉价、高效。并行化只是众多优化手段中的其中一种,并且只是 一种主要解决 CPU 为性能瓶颈的优化。
这些准则结合在一起,会让程序达到最大程度的加速倍数。前三个准则相互交织在一起,所以本节将着重分写这三个准则的交互关系。
请注意,这些准则也是需求说明的一部分。比如,加速倍速既是愿望、又是工作符合的绝对需求,或者说是运行环境。
理解这些设计准则之间的关系,对于权衡并行程序的各个设计目标十分有用。
- 程序在临界区上所花费的时间越少,潜在的加速倍速就越大。这是 Amdahl 定律的结果,这也是因为在一个时刻只能有一个 CPU 进入临界区的原因。更确切的说,程序在某个互斥的临界区上所耗费的时间必须大大小于 CPU 数的倒数,因为这样增加 CPU 数量才能达到事实上的加速。比如在 10 核系统上运行的程序只能在关键的临界区上花费少于 1/10 的时间,这样才能有效的扩展。
- 因为竞争所浪费的大量 CPU 或者时间,这些时间本来可以用于提高加速倍速,应该少于可用 CPU 的数目。CPU 数量和实际的加速倍速之间的差距越大,CPU 的使用率越低。同样,需要的效率越高,可以继续提升的加速倍速就越小。
- 如果使用的同步原语相较它们保护的临界区来说开销太大,那么加速程序运行的最佳办法是减少调用这些原语的次数(比如分批进入临界区、数据所有权、非对称同步、代码锁)。
- 如果临界区相较保护这块临界区的原语来说开销太大,那么加速程序运行的最佳办法是增加程序的并行化程度,比如使用读写锁、数据锁、非对称同步或数据所有权。
- 如果临界区相较保护这块临界区的原语来说开销太大,并且对受保护的数据结构读多于写,那么加速程序运行的最佳办法是增加程序的并行化程度,比如读写锁或非对称同步。
- 各种增加 SMP 性能的改动,比如减少锁竞争程度,能改善响应时间。
同步粒度
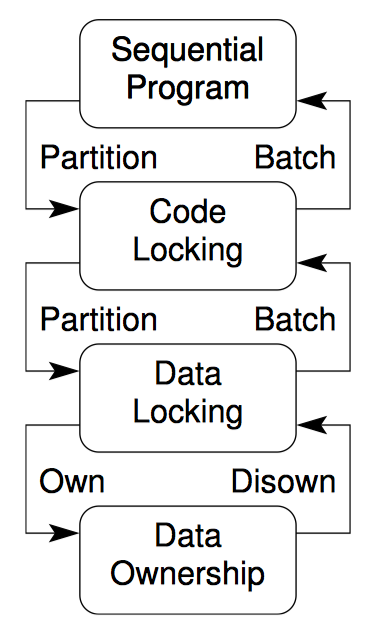
上图是对同步粒度不同层次的图形表示。每一种同步粒度都用一节内容来描述。
串行程序
如果程序在单处理器上运行足够快,并且不与其他进程、线程或者中断处理程序发生交互,那么你可以将代码中所有的同步原语删除,远离他们带来的开销和复杂性。好多年前曾有人争论摩尔定律最终会让所有程序变得如此,但是随着 2003 年以来 Intel CPU 的 CPU MIPS 和时钟频率增长速度的停止,此后要增加性能,就必须提高程序的并行化程度。是否这种趋势会导致一块芯片上继承几千个 CPU,这方面的争论不会很快停息,但是考虑本文作者 Paul 是在一台双核笔记本上敲下这句话的,SMP 的寿命极有可能比你我都长。另一个需要注意的地方是以太网的带宽持续增长。这种增长会进一步促进对多线程服务器的优化,这样才能有效处理通信载荷。

请注意,这并不意味着你应该在每个程序中都使用多线程方式编程。我再次说明,如果一个程序在单处理器上运行的很好,那么你就从 SMP 同步原语的开销和复杂性中解脱出来吧。
代码锁
代码锁是最简单的设计,仅使用全局锁。在已有的程序中使用代码锁,可以很容易让程序在多个处理器上运行。如果程序只有一个共享资源,那么代码锁的性能是最优的。但是,许多较大且复杂的程序会在临界区上执行多次,这就让代码锁的扩展性大大受限。
因此,最好在这样的程序中使用代码锁:只有一小段执行时间在临界区程序,或者对扩展性要求不高。在这种情况下,代码锁可以让程序相对简单,和单线程版本类似。
并且,代码锁尤其容易引起“锁竞争”,一种多个 CPU 并发访问同一把锁的情况。
数据锁
许多数据结构都可以分割,数据结构的每个部分带有一把自己的锁。这样虽然每个部分一次只能执行一个临界区,但是数据结构的各个部分形成的临界区就可以并行执行了。如果此时同步带来的开销不是主要瓶颈,那么可以使用数据来降低锁竞争程度。数据锁通过将一块过大的临界区分散到各个小的临界区来减少锁竞争,比如,维护哈希表中的 per-hash-bucket 临界区。不过这种扩展性的增强带来的是复杂性的少量提升,增加了额外的数据结构 struct bucket。
但是数据锁带来了和谐,在并行程序中,这总是意味着性能和扩展性的提升。因为这个原因,Sequent 在它的 DYNIX 和 DYNIX/ptx 操作系统中使用了数据锁。
不过,那些照顾过小孩的人可以证明,再细心的照料也不能保证一切风平浪静(多个小孩争抢一个玩具)。同样的情况也适用于 SMP 程序。比如,Linux 内核维护了一种文件和目录的缓存(dcache)。该缓存中的每个条目都有一把自己的锁。但是相较于其他条目,对应根目录的条目和它的直接后代更容易被遍历到。这将导致许多 CPU 竞争这些热门条目的锁。这就像虽然玩具有多个,但所有的孩子都要去挣同一个玩具。
在动态分配结构中,在许多情况下,可以设计算法来减少数据冲突的次数,某些情况下甚至可以完全消灭冲突(如 dcache)。数据锁通常用于分割像哈希表一样的数据结构,也适用于每个条目用某个数据结构的实例表示这种情况。
数据锁的关键挑战是对动态分配数据结构加锁,如何保证在获取锁时结构本身还存在。通过将锁放入静态分配且永不释放的哈希桶可以解决该挑战。但是这种手法不适用于哈希表大小可变的情况,所以锁也需要动态分配。在这种情况,还需要一些手段来阻止哈希桶在锁被获取之后的这段时间内释放。
数据所有权
数据所有权方法按照线程或者 CPU 的个数分割数据结构,在不需要任何同步开销的情况下,每个线程或者 CPU 都可以访问属于它的子集。但是如果线程 A 希望访问另一个线程 B 的数据,那么线程 A 是无法直接做到这一点。取而代之的是,线程 A 需要先与线程 B 通信,这样线程 B 以线程 A 的名义执行操作,或者另一种方法,将数据迁移到线程 A 上来。
数据所有权看起来很神秘,但是却应用得十分频繁:
- 任何只能被一个 CPU 或者一个线程访问的变量都属于这个 CPU 或者这个线程。
- 用户接口的实例拥有对应的用户上下文。这在与并行数据库引擎交互的应用程序中十分常见,让并行引擎看起来就像顺序执行的程序一样。这样应用程序拥有用户接口和当前操作。显式的并行化只在数据库引擎内部可见。
- 参数模拟,通常授予每个线程一段特定的参数区间,以此达到某种程度的并行化。有一些计算平台专门用来解决这类问题。
如果共享比较多,线程或者 CPU 间的通信会带来较大的复杂性和通信开销。不仅如此,如果最热的数据正好被一个 CPU 拥有,那么这个 CPU 就成了热点。不过,在不需要共享的情况下,数据所有权可以达到理想性能,代码也可以像顺序程序一样简单。最坏情况通常被称为尴尬的并行化。
另一个数据所有权的重要用法是当数据是只读时,这种情况下,所有线程可以通过复制来拥有数据。
并行快速路径
细粒度(通常能够带来更高的性能)的设计要比粗粒度的设计复杂。在许多情况下,一小部分代码带来了绝大部分开销。所以为什么不把精力放在这一小块代码上呢?
这就是并行快速路径设计模式背后的思想,尽可能并行化常见情况下的代码路径,同时不产生并行化整个算法所带来的复杂性。必须要理解这一点,不只是算法需要并行化,算法所属的工作负载也要并行化。构建这种并行快速路径,需要极大的创造性和设计上的努力。
并行快速路径结合了两种以上的设计模式,因此成为了一种模板设计模式。下列是并行快速路径结合其他设计模式的例子:
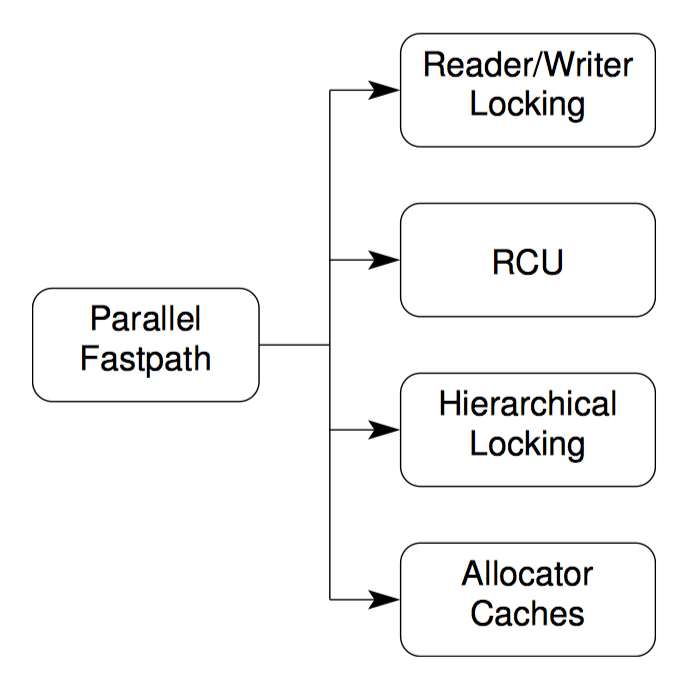
- 读写锁。
- Read-Copy-Update,大多作为读写锁的替代使用。
- 层次锁。
- 资源分配器缓存。
读写锁
如果同步开销可以忽略不计(比如程序使用了粗粒度的并行化),并且只有一小段临界区修改数据,那么让多个读者并行处理可以显著提升扩展性。写者与读者互斥,写者与另一写者也互斥。
读写锁是非对称锁的一种简单实例。Snaman 描述了一种在许多集群系统上使用的非对称锁,该锁有 6 种模式,其设计令人叹为观止。
层次锁
层次锁背后的思想是,在持有一把粗粒度锁时,同时再持有一把细粒度锁。这样一来,我们付出了获取第二把锁的开销,但是我们只持有它一小段时间。在这种情况下,简单的数据锁方法则更简单,而且性能更好。
资源分配器缓存
本节展示一种简明扼要的并行内存分配器,用于分配固定大小的内存。
并行资源分配问题
并行内存分配器锁面临的基本问题,是在大多数情况下快速地分配和释放内存,和在特殊情况下高效地分配和释放内存之间的矛盾。
假设有一个使用了数据所有权的程序——该程序简单地将内存按照 CPU 个数划分,这样每个 CPU 都有属于自己的一份内存。例如,该系统有 2 个 CPU 和 2G 内存。我们可以为每个 CPU 分配 1G 内存,这样每个 CPU 都可以访问属于自己的那一份内存,无需加锁,也不必关心由锁带来的复杂性和开销。可是这种简单的模型存在问题,如果有一种算法,需要让 CPU0 分配所有内存,让 CPU1 释放内存,就像生产者——消费者算法中的行为一样,这样该模型就失效了。
另一个极端,代码锁,则受到大量竞争和通信开销的影响。
资源分配的并行快速路径
常见的解决方案让每个 CPU 拥有一块规模适中的内存块缓存,以此作为快速路径,同时提供一块较大的共享内存池分配额外的内存块,该内存池使用代码锁加以保护。为了防止任何 CPU 独占内存块,我们给每个 CPU 的缓存可以容纳的内存块大小加以限制。在双核系统中,内存块的数据流如下图所示,当某个 CPU 的缓存池满时,该 CPU 释放的内存块被传送到全局缓存池中,类似的,当 CPU 缓存池为空时,该 CPU 所要分配的内存块也是从全局缓存池中取出来。

真实世界设计
虽然并行的玩具资源分配器非常简单,但是真实世界中的设计在几个方面上继续扩展了这个方案。
首先,真实的资源分配器需要处理各种不同的资源大小,在示例中只能分配固定的大小。一种比较流行的做法是提供一些列固定大小的资源,恰当地放置以平衡内碎片和外碎片,比如 20 世纪 80 年代后期的 BSD 内存分配器。这样做就意味着每种资源大小都要有一个“globalmem”变量,同样对应的锁也要每种一个,因此真实的实现将采用数据锁,而非玩具程序中的代码锁。
其次,产品级的系统必须可以改变内存的用途,这意味着这些系统必须能将内存块组合成更大的数据结构,比如页(page)。这种组合也需要锁的保护,这种锁必须是专属于每种资源大小的。
第三,组合后的内存必须回到内存管理系统,内存页也必须是从内存管理系统分配的。这一层面所需要的锁将依赖于内存管理系统,但也可以是代码锁。在这一层面中使用代码锁通常是可以容忍的,因为在设计良好的系统中很少触及这一级别。
尽管真实世界中的设计需要复杂许多,但背后的思想也是一样的——对并行快速路径这一原则的反复利用。以下是真实世界中的并行分配器类型:
| 等级 | 锁类型 | 目的 |
|---|---|---|
| 每线程资源池 | 数据所有权 | 高速分配 |
| 全局内存资源池 | 数据锁 | 将内存块放在各个线程中 |
| 组合 | 数据锁 | 将内存块放在页中 |
| 系统内存 | 代码锁 | 获取、释放系统内存 |
分割之外
本章讨论了如何运用数据分割这一思想,来设计既简单又能线性扩展的并行程序。运用分割和复制的主要目标是达到线性的加速倍数,换句话说,确保需要做的工作不会随着 CPU 或线程的增长而显著增长。通过分割或复制可以解决尴尬的并行问题,使其可以线性加速,但是我们还能做得更好吗?
为了回答这个问题,让我们来看一看迷宫问题。前年依赖,迷宫问题一直是一个令人着迷的研究对象,所以请读者不要感到意外,计算机可以生产并且解决迷宫问题,其中包括生物计算机、甚至是一些可插拔硬件。大学有时会将迷宫的并行解法布置成课程作业,作为展示并行计算框架优点的工具。
常见的解法是使用一个并行工作队列的算法(PWQ)。本节比较 PWQ 方法、串行解法(SEQ)、和使用了另一种并行算法的解法,这些方法都能解决任何随机生成的矩形迷宫问题。
略。
Feedback
Was this page helpful?
Glad to hear it! Please tell us how we can improve.
Sorry to hear that. Please tell us how we can improve.